Algebra
Algebra is the branch of mathematics that studies certain abstract systems, known as algebraic structures, and the manipulation of expressions within those systems. It is a generalization of arithmetic that introduces variables and algebraic operations other than the standard arithmetic operations, such as addition and multiplication.
Elementary algebra is the main form of algebra taught in schools. It examines mathematical statements using variables for unspecified values and seeks to determine for which values the statements are true. To do so, it uses different methods of transforming equations to isolate variables. Linear algebra is a closely related field that investigates linear equations and combinations of them called systems of linear equations. It provides methods to find the values that solve all equations in the system at the same time, and to study the set of these solutions.
Abstract algebra studies algebraic structures, which consist of a set of mathematical objects together with one or several operations defined on that set. It is a generalization of elementary and linear algebra, since it allows mathematical objects other than numbers and non-arithmetic operations. It distinguishes between different types of algebraic structures, such as groups, rings, and fields, based on the number of operations they use and the laws they follow, called axioms. Universal algebra and category theory provide general frameworks to investigate abstract patterns that characterize different classes of algebraic structures.
Algebraic methods were first studied in the ancient period to solve specific problems in fields like geometry. Subsequent mathematicians examined general techniques to solve equations independent of their specific applications. They described equations and their solutions using words and abbreviations until the 16th and 17th centuries, when a rigorous symbolic formalism was developed. In the mid-19th century, the scope of algebra broadened beyond a theory of equations to cover diverse types of algebraic operations and structures. Algebra is relevant to many branches of mathematics, such as geometry, topology, number theory, and calculus, and other fields of inquiry, like logic and the empirical sciences.
Definition and etymology
[edit]Algebra is the branch of mathematics that studies algebraic structures and the operations they use.[1] An algebraic structure is a non-empty set of mathematical objects, such as the integers, together with algebraic operations defined on that set, like addition and multiplication.[2][a] Algebra explores the laws, general characteristics, and types of algebraic structures. Within certain algebraic structures, it examines the use of variables in equations and how to manipulate these equations.[4][b]
Algebra is often understood as a generalization of arithmetic.[8] Arithmetic studies operations like addition, subtraction, multiplication, and division, in a particular domain of numbers, such as the real numbers.[9] Elementary algebra constitutes the first level of abstraction. Like arithmetic, it restricts itself to specific types of numbers and operations. It generalizes these operations by allowing indefinite quantities in the form of variables in addition to numbers.[10] A higher level of abstraction is found in abstract algebra, which is not limited to a particular domain and examines algebraic structures such as groups and rings. It extends beyond typical arithmetic operations by also covering other types of operations.[11] Universal algebra is still more abstract in that it is not interested in specific algebraic structures but investigates the characteristics of algebraic structures in general.[12]

The term "algebra" is sometimes used in a more narrow sense to refer only to elementary algebra or only to abstract algebra.[14] When used as a countable noun, an algebra is a specific type of algebraic structure that involves a vector space equipped with a certain type of binary operation.[15] Depending on the context, "algebra" can also refer to other algebraic structures, like a Lie algebra or an associative algebra.[16]
The word algebra comes from the Arabic term الجبر (al-jabr), which originally referred to the surgical treatment of bonesetting. In the 9th century, the term received a mathematical meaning when the Persian mathematician Muhammad ibn Musa al-Khwarizmi employed it to describe a method of solving equations and used it in the title of a treatise on algebra, al-Kitāb al-Mukhtaṣar fī Ḥisāb al-Jabr wal-Muqābalah [The Compendious Book on Calculation by Completion and Balancing] which was translated into Latin as Liber Algebrae et Almucabola.[c] The word entered the English language in the 16th century from Italian, Spanish, and medieval Latin.[18] Initially, its meaning was restricted to the theory of equations, that is, to the art of manipulating polynomial equations in view of solving them. This changed in the 19th century[d] when the scope of algebra broadened to cover the study of diverse types of algebraic operations and structures together with their underlying axioms, the laws they follow.[21]
Major branches
[edit]Elementary algebra
[edit]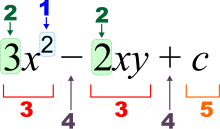
1 – power (exponent)
2 – coefficient
3 – term
4 – operator
5 – constant term
– constant
– variables
Elementary algebra, also called school algebra, college algebra, and classical algebra,[22] is the oldest and most basic form of algebra. It is a generalization of arithmetic that relies on variables and examines how mathematical statements may be transformed.[23]
Arithmetic is the study of numerical operations and investigates how numbers are combined and transformed using the arithmetic operations of addition, subtraction, multiplication, division, exponentiation, extraction of roots, and logarithm. For example, the operation of addition combines two numbers, called the addends, into a third number, called the sum, as in .[9]
Elementary algebra relies on the same operations while allowing variables in addition to regular numbers. Variables are symbols for unspecified or unknown quantities. They make it possible to state relationships for which one does not know the exact values and to express general laws that are true, independent of which numbers are used. For example, the equation belongs to arithmetic and expresses an equality only for these specific numbers. By replacing the numbers with variables, it is possible to express a general law that applies to any possible combination of numbers, like the commutative property of multiplication, which is expressed in the equation .[23]
Algebraic expressions are formed by using arithmetic operations to combine variables and numbers. By convention, the lowercase letters , , and represent variables. In some cases, subscripts are added to distinguish variables, as in , , and . The lowercase letters , , and are usually used for constants and coefficients.[e] The expression is an algebraic expression created by multiplying the number 5 with the variable and adding the number 3 to the result. Other examples of algebraic expressions are and .[25]
Some algebraic expressions take the form of statements that relate two expressions to one another. An equation is a statement formed by comparing two expressions, saying that they are equal. This can be expressed using the equals sign (), as in . Inequations involve a different type of comparison, saying that the two sides are different. This can be expressed using symbols such as the less-than sign (), the greater-than sign (), and the inequality sign (). Unlike other expressions, statements can be true or false, and their truth value usually depends on the values of the variables. For example, the statement is true if is either 2 or −2 and false otherwise.[26] Equations with variables can be divided into identity equations and conditional equations. Identity equations are true for all values that can be assigned to the variables, such as the equation . Conditional equations are only true for some values. For example, the equation is only true if is 5.[27]
The main goal of elementary algebra is to determine the values for which a statement is true. This can be achieved by transforming and manipulating statements according to certain rules. A key principle guiding this process is that whatever operation is applied to one side of an equation also needs to be done to the other side. For example, if one subtracts 5 from the left side of an equation one also needs to subtract 5 from the right side to balance both sides. The goal of these steps is usually to isolate the variable one is interested in on one side, a process known as solving the equation for that variable. For example, the equation can be solved for by adding 7 to both sides, which isolates on the left side and results in the equation .[28]
There are many other techniques used to solve equations. Simplification is employed to replace a complicated expression with an equivalent simpler one. For example, the expression can be replaced with the expression since by the distributive property.[29] For statements with several variables, substitution is a common technique to replace one variable with an equivalent expression that does not use this variable. For example, if one knows that then one can simplify the expression to arrive at . In a similar way, if one knows the value of one variable one may be able to use it to determine the value of other variables.[30]

Algebraic equations can be interpreted geometrically to describe spatial figures in the form of a graph. To do so, the different variables in the equation are understood as coordinates and the values that solve the equation are interpreted as points of a graph. For example, if is set to zero in the equation , then must be −1 for the equation to be true. This means that the -pair is part of the graph of the equation. The -pair , by contrast, does not solve the equation and is therefore not part of the graph. The graph encompasses the totality of -pairs that solve the equation.[31]
Polynomials
[edit]A polynomial is an expression consisting of one or more terms that are added or subtracted from each other, like . Each term is either a constant, a variable, or a product of a constant and variables. Each variable can be raised to a positive-integer power. A monomial is a polynomial with one term while two- and three-term polynomials are called binomials and trinomials. The degree of a polynomial is the maximal value (among its terms) of the sum of the exponents of the variables (4 in the above example).[32] Polynomials of degree one are called linear polynomials. Linear algebra studies systems of linear polynomials.[33] A polynomial is said to be univariate or multivariate, depending on whether it uses one or more variables.[34]
Factorization is a method used to simplify polynomials, making it easier to analyze them and determine the values for which they evaluate to zero. Factorization consists in rewriting a polynomial as a product of several factors. For example, the polynomial can be factorized as . The polynomial as a whole is zero if and only if one of its factors is zero, i.e., if is either −2 or 5.[35] Before the 19th century, much of algebra was devoted to polynomial equations, that is equations obtained by equating a polynomial to zero. The first attempts for solving polynomial equations were to express the solutions in terms of nth roots. The solution of a second-degree polynomial equation of the form is given by the quadratic formula[36] Solutions for the degrees 3 and 4 are given by the cubic and quartic formulas. There are no general solutions for higher degrees, as proven in the 19th century by the Abel–Ruffini theorem.[37] Even when general solutions do not exist, approximate solutions can be found by numerical tools like the Newton–Raphson method.[38]
The fundamental theorem of algebra asserts that every univariate polynomial equation of positive degree with real or complex coefficients has at least one complex solution. Consequently, every polynomial of a positive degree can be factorized into linear polynomials. This theorem was proved at the beginning of the 19th century, but this does not close the problem since the theorem does not provide any way for computing the solutions.[39]
Linear algebra
[edit]Linear algebra starts with the study systems of linear equations.[40] An equation is linear if it can be expressed in the form where , , ..., and are constants. Examples are and . A system of linear equations is a set of linear equations for which one is interested in common solutions.[41]
Matrices are rectangular arrays of values that have been originally introduced for having a compact and synthetic notation for systems of linear equations.[42] For example, the system of equations can be written as where and are the matrices
Under some conditions on the number of rows and columns, matrices can be added, multiplied, and sometimes inverted. All methods for solving linear systems may be expressed as matrix manipulations using these operations. For example, solving the above system consists of computing an inverted matrix such that where is the identity matrix. Then, multiplying on the left both members of the above matrix equation by one gets the solution of the system of linear equations as[43]
Methods of solving systems of linear equations range from the introductory, like substitution[44] and elimination,[45] to more advanced techniques using matrices, such as Cramer's rule, the Gaussian elimination, and LU decomposition.[46] Some systems of equations are inconsistent, meaning that no solutions exist because the equations contradict each other.[47][f] Consistent systems have either one unique solution or an infinite number of solutions.[48][g]
The study of vector spaces and linear maps form a large part of linear algebra. A vector space is an algebraic structure formed by a set with an addition that makes it an abelian group and a scalar multiplication that is compatible with addition (see vector space for details). A linear map is a function between vector spaces that is compatible with addition and scalar multiplication. In the case of finite-dimensional vector spaces, vectors and linear maps can be represented by matrices. It follows that the theories of matrices and finite-dimensional vector spaces are essentially the same. In particular, vector spaces provide a third way for expressing and manipulating systems of linear equations.[49] From this perspective, a matrix is a representation of a linear map: if one chooses a particular basis to describe the vectors being transformed, then the entries in the matrix give the results of applying the linear map to the basis vectors.[50]
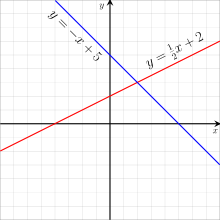
Systems of equations can be interpreted as geometric figures. For systems with two variables, each equation represents a line in two-dimensional space. The point where the two lines intersect is the solution of the full system because this is the only point that solves both the first and the second equation. For inconsistent systems, the two lines run parallel, meaning that there is no solution since they never intersect. If two equations are not independent then they describe the same line, meaning that every solution of one equation is also a solution of the other equation. These relations make it possible to seek solutions graphically by plotting the equations and determining where they intersect.[51] The same principles also apply to systems of equations with more variables, with the difference being that the equations do not describe lines but higher dimensional figures. For instance, equations with three variables correspond to planes in three-dimensional space, and the points where all planes intersect solve the system of equations.[52]
Abstract algebra
[edit]Abstract algebra, also called modern algebra,[53] is the study of algebraic structures. An algebraic structure is a framework for understanding operations on mathematical objects, like the addition of numbers. While elementary algebra and linear algebra work within the confines of particular algebraic structures, abstract algebra takes a more general approach that compares how algebraic structures differ from each other and what types of algebraic structures there are, such as groups, rings, and fields.[54] The key difference between these types of algebraic structures lies in the number of operations they use and the laws they obey.[55] In mathematics education, abstract algebra refers to an advanced undergraduate course that mathematics majors take after completing courses in linear algebra.[56]

On a formal level, an algebraic structure is a set[h] of mathematical objects, called the underlying set, together with one or several operations.[i] Abstract algebra is primarily interested in binary operations,[j] which take any two objects from the underlying set as inputs and map them to another object from this set as output.[60] For example, the algebraic structure has the natural numbers () as the underlying set and addition () as its binary operation.[58] The underlying set can contain mathematical objects other than numbers, and the operations are not restricted to regular arithmetic operations.[61] For instance, the underlying set of the symmetry group of a geometric object is made up of geometric transformations, such as rotations, under which the object remains unchanged. Its binary operation is function composition, which takes two transformations as input and has the transformation resulting from applying the first transformation followed by the second as its output.[62]
Group theory
[edit]Abstract algebra classifies algebraic structures based on the laws or axioms that its operations obey and the number of operations it uses. One of the most basic types is a group, which has one operation and requires that this operation is associative and has an identity element and inverse elements. An operation is associative if the order of several applications does not matter, i.e., if [k] is the same as for all elements. An operation has an identity element or a neutral element if one element e exists that does not change the value of any other element, i.e., if . An operation has inverse elements if for any element there exists a reciprocal element that undoes . If an element operates on its inverse then the result is the neutral element e, expressed formally as . Every algebraic structure that fulfills these requirements is a group.[64] For example, is a group formed by the set of integers together with the operation of addition. The neutral element is 0 and the inverse element of any number is .[65] The natural numbers with addition, by contrast, do not form a group since they contain only positive integers and therefore lack inverse elements.[66]
Group theory examines the nature of groups, with basic theorems such as the fundamental theorem of finite abelian groups and the Feit–Thompson theorem.[67] The latter was a key early step in one of the most important mathematical achievements of the 20th century: the collaborative effort, taking up more than 10,000 journal pages and mostly published between 1960 and 2004, that culminated in a complete classification of finite simple groups.[68]
Ring theory and field theory
[edit]A ring is an algebraic structure with two operations that work similarly to addition and multiplication of numbers and are named and generally denoted similarly. A ring is a commutative group under addition: the addition of the ring is associative, commutative, and has an identity element and inverse elements. The multiplication is associative and distributive with respect to addition; that is, and Moreover, multiplication is associative and has an identity element generally denoted as 1.[69][l] Multiplication needs not to be commutative; if it is commutative, one has a commutative ring.[71] The ring of integers () is one of the simplest commutative rings.[72]
A field is a commutative ring such that and each nonzero element has a multiplicative inverse.[73] The ring of integers does not form a field because it lacks multiplicative inverses. For example, the multiplicative inverse of is , which is not an integer. The rational numbers, the real numbers, and the complex numbers each form a field with the operations of addition and multiplication.[74]
Ring theory is the study of rings, exploring concepts such as subrings, quotient rings, polynomial rings, and ideals as well as theorems such as Hilbert's basis theorem.[75] Field theory is concerned with fields, examining field extensions, algebraic closures, and finite fields.[76] Galois theory explores the relation between field theory and group theory, relying on the fundamental theorem of Galois theory.[77]
Theories of interrelations among structures
[edit]
Besides groups, rings, and fields, there are many other algebraic structures studied by algebra. They include magmas, semigroups, monoids, abelian groups, commutative rings, modules, lattices, vector spaces, algebras over a field, and associative and non-associative algebras. They differ from each other in regard to the types of objects they describe and the requirements that their operations fulfill. Many are related to each other in that a basic structure can be turned into a more advanced structure by adding additional requirements.[55] For example, a magma becomes a semigroup if its operation is associative.[78]
Homomorphisms are tools to examine structural features by comparing two algebraic structures.[79] A homomorphism is a function from the underlying set of one algebraic structure to the underlying set of another algebraic structure that preserves certain structural characteristics. If the two algebraic structures use binary operations and have the form and then the function is a homomorphism if it fulfills the following requirement: . The existence of a homomorphism reveals that the operation in the second algebraic structure plays the same role as the operation does in the first algebraic structure.[80] Isomorphisms are a special type of homomorphism that indicates a high degree of similarity between two algebraic structures. An isomorphism is a bijective homomorphism, meaning that it establishes a one-to-one relationship between the elements of the two algebraic structures. This implies that every element of the first algebraic structure is mapped to one unique element in the second structure without any unmapped elements in the second structure.[81]
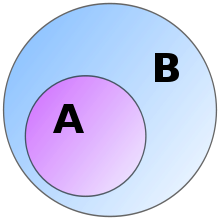
Another tool of comparison is the relation between an algebraic structure and its subalgebra.[82] The algebraic structure and its subalgebra use the same operations,[m] which follow the same axioms. The only difference is that the underlying set of the subalgebra is a subset of the underlying set of the algebraic structure.[n] All operations in the subalgebra are required to be closed in its underlying set, meaning that they only produce elements that belong to this set.[82] For example, the set of even integers together with addition is a subalgebra of the full set of integers together with addition. This is the case because the sum of two even numbers is again an even number. But the set of odd integers together with addition is not a subalgebra because it is not closed: adding two odd numbers produces an even number, which is not part of the chosen subset.[83]
Universal algebra is the study of algebraic structures in general. As part of its general perspective, it is not concerned with the specific elements that make up the underlying sets and considers operations with more than two inputs, such as ternary operations. It provides a framework for investigating what structural features different algebraic structures have in common.[85][o] One of those structural features concerns the identities that are true in different algebraic structures. In this context, an identity is a universal equation or an equation that is true for all elements of the underlying set. For example, commutativity is a universal equation that states that is identical to for all elements.[87] A variety is a class of all algebraic structures that satisfy certain identities. For example, if two algebraic structures satisfy commutativity then they are both part of the corresponding variety.[88][p][q]
Category theory examines how mathematical objects are related to each other using the concept of categories. A category is a collection of objects together with a collection of morphisms or "arrows" between those objects. These two collections must satisfy certain conditions. For example, morphisms can be joined, or composed: if there exists a morphism from object to object , and another morphism from object to object , then there must also exist one from object to object . Composition of morphisms is required to be associative, and there must be an "identity morphism" for every object.[92] Categories are widely used in contemporary mathematics since they provide a unifying framework to describe and analyze many fundamental mathematical concepts. For example, sets can be described with the category of sets, and any group can be regarded as the morphisms of a category with just one object.[93]
History
[edit]
The origin of algebra lies in attempts to solve mathematical problems involving arithmetic calculations and unknown quantities. These developments happened in the ancient period in Babylonia, Egypt, Greece, China, and India. One of the earliest documents on algebraic problems is the Rhind Mathematical Papyrus from ancient Egypt, which was written around 1650 BCE.[r] It discusses solutions to linear equations, as expressed in problems like "A quantity; its fourth is added to it. It becomes fifteen. What is the quantity?" Babylonian clay tablets from around the same time explain methods to solve linear and quadratic polynomial equations, such as the method of completing the square.[95]
Many of these insights found their way to the ancient Greeks. Starting in the 6th century BCE, their main interest was geometry rather than algebra, but they employed algebraic methods to solve geometric problems. For example, they studied geometric figures while taking their lengths and areas as unknown quantities to be determined, as exemplified in Pythagoras' formulation of the difference of two squares method and later in Euclid's Elements.[96] In the 3rd century CE, Diophantus provided a detailed treatment of how to solve algebraic equations in a series of books called Arithmetica. He was the first to experiment with symbolic notation to express polynomials.[97] Diophantus's work influenced Arab development of algebra with many of his methods reflected in the concepts and techniques used in medieval Arabic algebra.[98] In ancient China, The Nine Chapters on the Mathematical Art, a book composed over the period spanning from the 10th century BCE to the 2nd century CE,[99] explored various techniques for solving algebraic equations, including the use of matrix-like constructs.[100]
There is no unanimity as to whether these early developments are part of algebra or only precursors. They offered solutions to algebraic problems but did not conceive them in an abstract and general manner, focusing instead on specific cases and applications.[101] This changed with the Persian mathematician al-Khwarizmi,[s] who published his The Compendious Book on Calculation by Completion and Balancing in 825 CE. It presents the first detailed treatment of general methods that can be used to manipulate linear and quadratic equations by "reducing" and "balancing" both sides.[103] Other influential contributions to algebra came from the Arab mathematician Thābit ibn Qurra also in the 9th century and the Persian mathematician Omar Khayyam in the 11th and 12th centuries.[104]
In India, Brahmagupta investigated how to solve quadratic equations and systems of equations with several variables in the 7th century CE. Among his innovations were the use of zero and negative numbers in algebraic equations.[105] The Indian mathematicians Mahāvīra in the 9th century and Bhāskara II in the 12th century further refined Brahmagupta's methods and concepts.[106] In 1247, the Chinese mathematician Qin Jiushao wrote the Mathematical Treatise in Nine Sections, which includes an algorithm for the numerical evaluation of polynomials, including polynomials of higher degrees.[107]
The Italian mathematician Fibonacci brought al-Khwarizmi's ideas and techniques to Europe in books including his Liber Abaci.[108] In 1545, the Italian polymath Gerolamo Cardano published his book Ars Magna, which covered many topics in algebra, discussed imaginary numbers, and was the first to present general methods for solving cubic and quartic equations.[109] In the 16th and 17th centuries, the French mathematicians François Viète and René Descartes introduced letters and symbols to denote variables and operations, making it possible to express equations in an abstract and concise manner. Their predecessors had relied on verbal descriptions of problems and solutions.[110] Some historians see this development as a key turning point in the history of algebra and consider what came before it as the prehistory of algebra because it lacked the abstract nature based on symbolic manipulation.[111]
In the 17th and 18th centuries, many attempts were made to find general solutions to polynomials of degree five and higher. All of them failed.[37] At the end of the 18th century, the German mathematician Carl Friedrich Gauss proved the fundamental theorem of algebra, which describes the existence of zeros of polynomials of any degree without providing a general solution.[19] At the beginning of the 19th century, the Italian mathematician Paolo Ruffini and the Norwegian mathematician Niels Henrik Abel were able to show that no general solution exists for polynomials of degree five and higher.[37] In response to and shortly after their findings, the French mathematician Évariste Galois developed what came later to be known as Galois theory, which offered a more in-depth analysis of the solutions of polynomials while also laying the foundation of group theory.[20] Mathematicians soon realized the relevance of group theory to other fields and applied it to disciplines like geometry and number theory.[112]

Starting in the mid-19th century, interest in algebra shifted from the study of polynomials associated with elementary algebra towards a more general inquiry into algebraic structures, marking the emergence of abstract algebra. This approach explored the axiomatic basis of arbitrary algebraic operations.[113] The invention of new algebraic systems based on different operations and elements accompanied this development, such as Boolean algebra, vector algebra, and matrix algebra.[114] Influential early developments in abstract algebra were made by the German mathematicians David Hilbert, Ernst Steinitz, and Emmy Noether as well as the Austrian mathematician Emil Artin. They researched different forms of algebraic structures and categorized them based on their underlying axioms into types, like groups, rings, and fields.[115]
The idea of the even more general approach associated with universal algebra was conceived by the English mathematician Alfred North Whitehead in his 1898 book A Treatise on Universal Algebra. Starting in the 1930s, the American mathematician Garrett Birkhoff expanded these ideas and developed many of the foundational concepts of this field.[116] The invention of universal algebra led to the emergence of various new areas focused on the algebraization of mathematics—that is, the application of algebraic methods to other branches of mathematics. Topological algebra arose in the early 20th century, studying algebraic structures such as topological groups and Lie groups.[117] In the 1940s and 50s, homological algebra emerged, employing algebraic techniques to study homology.[118] Around the same time, category theory was developed and has since played a key role in the foundations of mathematics.[119] Other developments were the formulation of model theory and the study of free algebras.[120]
Applications
[edit]The influence of algebra is wide-reaching, both within mathematics and in its applications to other fields.[121] The algebraization of mathematics is the process of applying algebraic methods and principles to other branches of mathematics, such as geometry, topology, number theory, and calculus. It happens by employing symbols in the form of variables to express mathematical insights on a more general level, allowing mathematicians to develop formal models describing how objects interact and relate to each other.[122]

One application, found in geometry, is the use of algebraic statements to describe geometric figures. For example, the equation describes a line in two-dimensional space while the equation corresponds to a sphere in three-dimensional space. Of special interest to algebraic geometry are algebraic varieties,[t] which are solutions to systems of polynomial equations that can be used to describe more complex geometric figures.[124] Algebraic reasoning can also solve geometric problems. For example, one can determine whether and where the line described by intersects with the circle described by by solving the system of equations made up of these two equations.[125] Topology studies the properties of geometric figures or topological spaces that are preserved under operations of continuous deformation. Algebraic topology relies on algebraic theories such as group theory to classify topological spaces. For example, homotopy groups classify topological spaces based on the existence of loops or holes in them.[126]
Number theory is concerned with the properties of and relations between integers. Algebraic number theory applies algebraic methods and principles to this field of inquiry. Examples are the use of algebraic expressions to describe general laws, like Fermat's Last Theorem, and of algebraic structures to analyze the behavior of numbers, such as the ring of integers.[127] The related field of combinatorics uses algebraic techniques to solve problems related to counting, arrangement, and combination of discrete objects. An example in algebraic combinatorics is the application of group theory to analyze graphs and symmetries.[128] The insights of algebra are also relevant to calculus, which uses mathematical expressions to examine rates of change and accumulation. It relies on algebra, for instance, to understand how these expressions can be transformed and what role variables play in them.[129] Algebraic logic employs the methods of algebra to describe and analyze the structures and patterns that underlie logical reasoning,[130] exploring both the relevant mathematical structures themselves and their application to concrete problems of logic.[131] It includes the study of Boolean algebra to describe propositional logic[132] as well as the formulation and analysis of algebraic structures corresponding to more complex systems of logic.[133]

Algebraic methods are also commonly employed in other areas, like the natural sciences. For example, they are used to express scientific laws and solve equations in physics, chemistry, and biology.[135] Similar applications are found in fields like economics, geography, engineering (including electronics and robotics), and computer science to express relationships, solve problems, and model systems.[136] Linear algebra plays a central role in artificial intelligence and machine learning, for instance, by enabling the efficient processing and analysis of large datasets.[137] Various fields rely on algebraic structures investigated by abstract algebra. For example, physical sciences like crystallography and quantum mechanics make extensive use of group theory,[138] which is also employed to study puzzles such as Sudoku and Rubik's cubes,[139] and origami.[140] Both coding theory and cryptology rely on abstract algebra to solve problems associated with data transmission, like avoiding the effects of noise and ensuring data security.[141]
Education
[edit]
Algebra education mostly focuses on elementary algebra, which is one of the reasons why elementary algebra is also called school algebra. It is usually not introduced until secondary education since it requires mastery of the fundamentals of arithmetic while posing new cognitive challenges associated with abstract reasoning and generalization.[143] It aims to familiarize students with the formal side of mathematics by helping them understand mathematical symbolism, for example, how variables can be used to represent unknown quantities. An additional difficulty for students lies in the fact that, unlike arithmetic calculations, algebraic expressions are often difficult to solve directly. Instead, students need to learn how to transform them according to certain laws, often with the goal of determining an unknown quantity.[144]
Some tools to introduce students to the abstract side of algebra rely on concrete models and visualizations of equations, including geometric analogies, manipulatives including sticks or cups, and "function machines" representing equations as flow diagrams. One method uses balance scales as a pictorial approach to help students grasp basic problems of algebra. The mass of some objects on the scale is unknown and represents variables. Solving an equation corresponds to adding and removing objects on both sides in such a way that the sides stay in balance until the only object remaining on one side is the object of unknown mass.[145] Word problems are another tool to show how algebra is applied to real-life situations. For example, students may be presented with a situation in which Naomi's brother has twice as many apples as Naomi. Given that both together have twelve apples, students are then asked to find an algebraic equation that describes this situation () and to determine how many apples Naomi has ().[146]
At the university level, mathematics students encounter advanced algebra topics from linear and abstract algebra. Initial undergraduate courses in linear algebra focus on matrices, vector spaces, and linear maps. Upon completing them, students are usually introduced to abstract algebra, where they learn about algebraic structures like groups, rings, and fields, as well as the relations between them. The curriculum typically also covers specific instances of algebraic structures, such as the systems of the rational numbers, the real numbers, and the polynomials.[147]
See also
[edit]- Algebra over a set – Algebraic concept in measure theory, also referred to as an algebra of sets
- Algebra tile – Type of mathematical manipulative
- Algebraic combinatorics – Area of combinatorics
- C*-algebra – Topological complex vector space
- Clifford algebra – Algebra based on a vector space with a quadratic form
- Commutative algebra – Branch of algebra that studies commutative rings
- Composition algebra – Type of algebras, possibly non associative
- Computer algebra – Scientific area at the interface between computer science and mathematics
- Cyclotomic polynomial – Irreducible polynomial whose roots are nth roots of unity
- Diophantine equation – Polynomial equation whose integer solutions are sought
- Discrete group – Type of topological group
- Dual space – In mathematics, vector space of linear forms
- Eigenvalues and eigenvectors – Concepts from linear algebra
- Equivalence class – Mathematical concept
- Equivalence relation – Mathematical concept for comparing objects
- Exterior algebra – Algebra associated to any vector space
- F-algebra
- Finite field – Algebraic structure
- Fundamental theorem of finitely generated abelian groups – Commutative group where every element is the sum of elements from one finite subset
- Geometric algebra – Algebraic structure designed for geometry
- Heyting algebra – Algebraic structure used in logic
- Hilbert space – Type of topological vector space
- Hilbert's Nullstellensatz – Relation between algebraic varieties and polynomial ideals
- Hilbert's syzygy theorem – Theorem about linear relations in ideals and modules over polynomial rings
- Hopf algebra – Construction in algebra
- Lattice (group) – Periodic set of points
- Lie group – Group that is also a differentiable manifold with group operations that are smooth
- Linear form – Linear map from a vector space to its field of scalars
- Linear subspace – In mathematics, vector subspace
- Matrix decomposition – Representation of a matrix as a product
- Multilinear map – Vector-valued function of multiple vectors, linear in each argument
- Non-associative algebra – Algebra over a field where binary multiplication is not necessarily associative
- Outline of algebra – Overview of and topical guide to algebra
- Quaternion – Noncommutative extension of the complex numbers
- Rational function – Ratio of polynomial functions
- Relational algebra – Theory of relational databases
- Representation theory – Branch of mathematics that studies abstract algebraic structures
- Root of unity – Number that has an integer power equal to 1
- Scheme theory – Generalization of algebraic variety
- Sigma-algebra – Algebraic structure of set algebra
- Singular value decomposition – Matrix decomposition
- Spectral theory – Collection of mathematical theories
- Symmetric algebra – "Smallest" commutative algebra that contains a vector space
- T-algebra – Operation in algebra and mathematics
- Tensor – Algebraic object with geometric applications
- Tensor algebra – Universal construction in multilinear algebra
- Wiles' proof of Fermat's Last Theorem – 1995 publication in mathematics
References
[edit]Notes
[edit]- ^ When understood in the widest sense, an algebraic operation is a function from a Cartesian power of a set into that set, expressed formally as . Addition of real numbers is an example of an algebraic operation: it takes two numbers as input and produces one number as output. It has the form .[3]
- ^ Algebra is covered by division 512 in the Dewey Decimal Classification[5] and subclass QA 150-272.5 in the Library of Congress Classification.[6] It encompasses several areas in the Mathematics Subject Classification.[7]
- ^ The exact meaning of the term al-jabr in al-Khwarizmi's work is disputed. In some passages, it expresses that a quantity diminished by subtraction is restored to its original value, similar to how a bonesetter restores broken bones by bringing them into proper alignment.[17]
- ^ These changes were in part triggered by discoveries that solved many of the older problems of algebra. For example, the proof of the fundamental theorem of algebra demonstrated the existence of complex solutions of polynomials[19] and the introduction of Galois theory characterized the polynomials that have general solutions.[20]
- ^ Constants represent fixed numbers that do not change during the study of a specific problem.[24]
- ^ For example, the equations and contradict each other since no values of and exist that solve both equations at the same time.[47]
- ^ Whether a consistent system of equations has a unique solution depends on the number of variables and independent equations. Several equations are independent of each other if they do not provide the same information and cannot be derived from each other. A unique solution exists if the number of variables is the same as the number of independent equations. Underdetermined systems, by contrast, have more variables than independent equations and have an infinite number of solutions if they are consistent.[48]
- ^ A set is an unordered collection of distinct elements, such as numbers, vectors, or other sets. Set theory describes the laws and properties of sets.[57]
- ^ According to some definitions, algebraic structures include a distinguished element as an additional component, such as the identity element in the case of multiplication.[58]
- ^ Some of the algebraic structures studied by abstract algebra include unary operations in addition to binary operations. For example, normed vector spaces have a norm, which is a unary operation often used to associate a vector with its length.[59]
- ^ The symbols and are used in this article to represent any operation that may or may not resemble arithmetic operations.[63]
- ^ Some authors do not require the existence of multiplicative identity elements. A ring without multiplicative identity is sometimes called a rng.[70]
- ^ According to some definitions, it is also possible for a subalgebra to have fewer operations.[83]
- ^ This means that all the elements of the first set are also elements of the second set but the second set may contain elements not found in the first set.[84]
- ^ A slightly different approach understands universal algebra as the study of one type of algebraic structures known as universal algebras. Universal algebras are defined in a general manner to include most other algebraic structures. For example, groups and rings are special types of universal algebras.[86]
- ^ Not every type of algebraic structure forms a variety. For example, both groups and rings form varieties but fields do not.[89]
- ^ Besides identities, universal algebra is also interested in structural features associated with quasi-identities. A quasi-identity is an identity that only needs to be present under certain conditions (which take the form of a Horn clause[90]). It is a generalization of identity in the sense that every identity is a quasi-identity but not every quasi-identity is an identity. A quasivariety is a class of all algebraic structures that satisfy certain quasi-identities.[91]
- ^ The exact date is disputed and some historians suggest a later date around 1550 BCE.[94]
- ^ Some historians consider him the "father of algebra" while others reserve this title for Diophantus.[102]
- ^ Algebraic varieties studied in geometry differ from the more general varieties studied in universal algebra.[123]
Citations
[edit]- ^
- Merzlyakov & Shirshov 2020, Lead section
- Gilbert & Nicholson 2004, p. 4
- ^
- Fiche & Hebuterne 2013, p. 326
- Merzlyakov & Shirshov 2020, § The Subject Matter of Algebra, Its Principal Branches and Its Connection with Other Branches of Mathematics.
- Gilbert & Nicholson 2004, p. 4
- ^ Baranovich 2023, Lead section
- ^
- Pratt 2022, Lead section, § 1. Elementary Algebra, § 2. Abstract Algebra, § 3. Universal Algebra
- Merzlyakov & Shirshov 2020, § The Subject Matter of Algebra, Its Principal Branches and Its Connection with Other Branches of Mathematics.
- ^ Higham 2019, p. 296
- ^ Library of Congress, p. 3
- ^ zbMATH Open 2024
- ^
- Maddocks 2008, p. 129
- Burgin 2022, p. 45
- ^ a b
- ^
- Maddocks 2008, pp. 129–130
- Pratt 2022, Lead section, § 1. Elementary Algebra
- Wagner & Kieran 2018, p. 225
- ^
- Maddocks 2008, pp. 131–132
- Pratt 2022, Lead section, § 2. Abstract Algebra
- Wagner & Kieran 2018, p. 225
- ^
- Pratt 2022, § 3. Universal Algebra
- Grillet 2007, p. 559
- Denecke & Wismath 2018, p. v
- Cohn 2012, p. xiii
- ^
- Cresswell 2010, p. 11
- OUP Staff
- Menini & Oystaeyen 2017, p. 722
- ^
- Weisstein 2003, p. 46
- Walz 2016, Algebra
- ^
- Weisstein 2003, p. 46
- Brešar 2014, p. xxxiii
- Golan 1995, pp. 219–227
- ^ EoM Staff 2017
- ^
- Oaks & Alkhateeb 2007, pp. 45–46, 58
- Gandz 1926, p. 437
- ^
- Cresswell 2010, p. 11
- OUP Staff
- Menini & Oystaeyen 2017, p. 722
- Hoad 1993, p. 10
- ^ a b
- Tanton 2005, p. 10
- Kvasz 2006, p. 308
- Corry 2024, § The Fundamental Theorem of Algebra
- ^ a b
- Kvasz 2006, pp. 314–345
- Merzlyakov & Shirshov 2020, § Historical Survey
- Corry 2024, § Galois Theory, § Applications of Group Theory
- ^
- Tanton 2005, p. 10
- Corry 2024, § Structural Algebra
- Hazewinkel 1994, pp. 73–74
- ^
- ^ a b
- Maddocks 2008, p. 129
- Berggren 2015, Lead section
- Pratt 2022, § 1. Elementary Algebra
- Merzlyakov & Shirshov 2020, § 1. Historical Survey
- ^ Sobolev 2015
- ^
- Maddocks 2008, pp. 129–130
- Young 2010, p. 999
- Majewski 2004, p. 347
- Pratt 2022, § 1. Elementary Algebra
- Sorell 2000, p. 19
- ^
- Maddocks 2008, pp. 129–130
- Tsokos & Wooten 2015, p. 451
- Mishra 2016, p. 1.2
- ^
- ^
- Maddocks 2008, p. 130
- McKeague 1986, pp. 51–54
- Pratt 2022, § 1. Elementary Algebra
- Merzlyakov & Shirshov 2020, § 1. Historical Survey
- ^
- ^
- Berggren 2015, § Solving Systems of Algebraic Equations
- McKeague 2014, p. 386
- McKeague 1986, p. 148
- ^
- Maddocks 2008, pp. 130–131
- Rohde et al. 2012, p. 89
- Walz 2016, Algebra
- ^
- Bracken & Miller 2014, pp. 386–387
- Kaufmann & Schwitters 2011, p. 220
- Markushevich 2015
- ^
- Sahai & Bist 2002, p. 21
- Maddocks 2008, p. 131
- Barrera-Mora 2023, pp. ix, 1–2
- ^ Geddes, Czapor & Labahn 2007, p. 46
- ^
- Lukas 2022, pp. 47–49
- Berggren 2015, § Algebraic Expressions, § Solving Algebraic Equations
- ^
- Berggren 2015, § Solving algebraic equations
- Corry 2024, § Classical algebra
- ^ a b c
- Tanton 2005, p. 10
- Merzlyakov & Shirshov 2020, § Historical Survey
- Corry 2024, § Impasse with Radical Methods
- ^ Igarashi et al. 2014, p. 103
- ^
- Berggren 2015, § Solving algebraic equations
- Tanton 2005, p. 10
- Kvasz 2006, p. 308
- Corry 2024, § The Fundamental Theorem of Algebra
- ^
- Maddocks 2008, p. 131
- Barrera-Mora 2023, pp. ix, 1–2,
- ^
- Anton & Rorres 2013, pp. 2–3
- Maddocks 2008, p. 131
- Voitsekhovskii 2011
- ^
- Saikia 2008, p. 1
- Lal 2017, p. 31
- Mirakhor & Krichene 2014, p. 107
- ^
- Brown 2015, pp. 30–31
- Waerden 2003, pp. 70–72
- ^
- Young 2010, pp. 697–698
- Maddocks 2008, p. 131
- Sullivan 2010, pp. 53–54
- ^
- Anton & Rorres 2013, pp. 7–8
- Sullivan 2010, pp. 55–56
- Atanasiu & Mikusinski 2019, p. 75
- ^
- Maddocks 2008, p. 131
- Anton & Rorres 2013, pp. 7–8, 11, 491
- ^ a b
- Anton & Rorres 2013, pp. 3–7
- Mortensen 2013, pp. 73–74
- Young 2023, pp. 714–715
- ^ a b
- Maddocks 2008, p. 131
- Harrison & Waldron 2011, p. 464
- Anton 2013, p. 255
- ^
- ^
- Solomon 2014, p. 57
- Ricardo 2009, pp. 395–396
- ^
- Anton & Rorres 2013, pp. 3–5
- Young 2010, pp. 696–697
- Sneyd, Fewster & McGillivray 2022, p. 211
- ^
- Anton & Rorres 2013, pp. 3–5
- Young 2010, p. 713
- Sneyd, Fewster & McGillivray 2022, p. 211
- ^
- Gilbert & Nicholson 2004, p. 1
- Dominich 2008, p. 19
- ^
- Maddocks 2008, pp. 131–132
- Pratt 2022, Lead section, § 2. Abstract Algebra
- Gilbert & Nicholson 2004, pp. 1–3
- Dominich 2008, p. 19
- ^ a b
- Pratt 2022, Lead section, § 2. Abstract Algebra
- Merzlyakov & Shirshov 2020, The Subject Matter of Algebra, Its Principal Branches and Its Connection with Other Branches of Mathematics.
- Bourbaki 1998, pp. 428–430, 446
- ^ Hausberger 2020, Abstract Algebra Teaching and Learning
- ^
- Tanton 2005, p. 460
- Murthy 2012, p. 1.3
- ^ a b Ovchinnikov 2015, p. 27
- ^ Grillet 2007, p. 247
- ^
- Whitelaw 1995, p. 61
- Nicholson 2012, p. 70
- Fiche & Hebuterne 2013, p. 326
- Pratt 2022, Lead section, § 2. Abstract Algebra
- ^
- Maddocks 2008, pp. 131–132
- Pratt 2022, Lead section, § 2. Abstract Algebra
- ^
- Olver 1999, pp. 55–56
- Abas & Salman 1994, pp. 58–59
- Häberle 2009, p. 640
- ^ Gilbert & Nicholson 2004, p. 4
- ^
- Kargapolov & Merzlyakov 2016, § Definition
- Khattar & Agrawal 2023, pp. 4–6
- Maddocks 2008, pp. 131–132
- Pratt 2022, Lead section, § 2. Abstract Algebra
- Neri 2019, p. 258
- ^
- Khattar & Agrawal 2023, pp. 6–7
- Maddocks 2008, pp. 131–132
- Adhikari & Adhikari 2013, p. 72
- ^
- McWeeny 2002, p. 6
- Kramer & Pippich 2017, p. 49
- ^
- Tanton 2005, p. 242
- Bhattacharya, Jain & Nagpaul 1994, p. 141
- Weisstein 2003, p. 1020
- ^
- Elwes 2006
- Wilson 2009, p. 2
- ^
- Weisstein 2003, p. 2579
- Maxwell 2009, pp. 73–74
- Pratt 2022, § 2.3 Rings
- ^ Silverman 2022, p. 64
- ^ Geddes, Czapor & Labahn 2007, p. 24
- ^ Smith 2015, p. 161
- ^
- Geddes, Czapor & Labahn 2007, p. 24
- Weisstein 2003, pp. 1047, 2579
- Pratt 2022, § 2.4 Fields
- ^
- Irving 2004, pp. 77, 236
- Weisstein 2003, pp. 1047, 2579
- Hohn 2013, pp. 83–84
- ^
- Serovajsky 2020, § Room 4B.5 Rings
- Kleiner 2007, p. 63
- Kline 1990, p. 1153
- ^
- Waerden 2003, pp. 110–114, 231, 246
- Karpilovsky 1989, p. 45
- Kleiner 2007, p. 63
- ^
- ^ Cooper 2011, p. 60
- ^
- Rowen 2006, p. 12
- Pratt 2022, § 3.3 Birkhoff's Theorem
- Grätzer 2008, p. 34
- ^
- Pratt 2022, § 3.3 Birkhoff's Theorem
- Rowen 2006, p. 12
- Gowers, Barrow-Green & Leader 2010, pp. 27–28
- Adhikari 2016, pp. 5–6
- ^
- ^ a b
- Indurkhya 2013, pp. 217–218
- Pratt 2022, § 3.3 Birkhoff's Theorem
- Grätzer 2008, p. 34
- ^ a b Indurkhya 2013, pp. 217–218
- ^ Efimov 2014
- ^
- Pratt 2022, § 3. Universal Algebra
- Cohn 2012, p. xiii
- ^
- Smirnov 2020
- Grätzer 2008, pp. 7–8
- Bahturin 2013, p. 346
- ^
- Pratt 2022, § 3.2 Equational Logic
- Mal’cev 1973, pp. 210–211
- ^
- Mal’cev 1973, pp. 210–211
- Cohn 2012, p. 162
- Rosen 2012, p. 779
- Hazewinkel 1994, p. 406
- ^ Cohn 1995, p. 8
- ^ Mal’cev 1973, p. 211
- ^
- Mal’cev 1973, pp. 210–211
- Pratt 2022, § 3. Universal Algebra
- Artamonov 2003, p. 873
- ^
- Weisstein 2003, pp. 347–348
- Gowers, Barrow-Green & Leader 2010, pp. 6, 165
- Cheng 2023, p. 102
- ^
- Gowers, Barrow-Green & Leader 2010, pp. 6, 165
- Borceux 1994, p. 20
- Laos 1998, p. 100
- Cheng 2023, pp. 128–131
- ^
- Corry 2024, § Problem Solving in Egypt and Babylon
- Brezinski, Meurant & Redivo-Zaglia 2022, p. 34
- ^
- Tanton 2005, p. 9
- Kvasz 2006, p. 290
- Corry 2024, § Problem Solving in Egypt and Babylon
- ^
- Tanton 2005, p. 9
- Kvasz 2006, p. 290
- Corry 2024, § The Pythagoreans and Euclid
- ^
- Merzlyakov & Shirshov 2020, § Historical Survey
- Sialaros 2018, p. 55
- Corry 2024, § Diophantus
- ^
- Hettle 2015, pp. 139–141, 160–161
- Christianidis & Megremi 2019, pp. 16–17
- ^ Burgin 2022, p. 10
- ^ Higgins 2015, p. 89
- ^
- Kvasz 2006, pp. 290–291
- Sialaros 2018, p. 55
- Boyer & Merzbach 2011, p. 161
- Derbyshire 2006, p. 31
- ^
- ^
- Tanton 2005, p. 10
- Kvasz 2006, pp. 291–293
- Merzlyakov & Shirshov 2020, § Historical Survey
- ^
- Waerden 2013, pp. 3, 15–16, 24–25
- Jenkins 2010, p. 82
- Pickover 2009, p. 90
- ^
- Tanton 2005, pp. 9–10
- Corry 2024, § The Equation in India and China
- ^
- ^
- Smorynski 2007, p. 137
- Zwillinger 2002, p. 812
- ^
- Waerden 2013, pp. 32–35
- Tanton 2005, p. 10
- Kvasz 2006, p. 293
- ^
- Tanton 2005, p. 10
- Kvasz 2006, p. 293
- Corry 2024, § Cardano and the Solving of Cubic and Quartic Equations
- Miyake 2002, p. 268
- ^
- Tanton 2005, p. 10
- Kvasz 2006, pp. 291–292, 297–298, 302
- Merzlyakov & Shirshov 2020, § Historical Survey
- Corry 2024, § Viète and the Formal Equation, § Analytic Geometry
- ^
- Hazewinkel 1994, p. 73
- Merzlyakov & Shirshov 2020, § Historical Survey
- ^
- Corry 2024, § Applications of Group Theory
- Bueno & French 2018, pp. 73–75
- ^
- Merzlyakov & Shirshov 2020, § Historical Survey
- Tanton 2005, p. 10
- Corry 2024, § Structural Algebra
- Hazewinkel 1994, pp. 73–74
- ^
- Merzlyakov & Shirshov 2020, § Historical Survey
- Tanton 2005, p. 10
- Corry 2024, § Matrices, § Quaternions and Vectors
- ^
- Merzlyakov & Shirshov 2020, § Historical Survey
- Corry 2024, § Hilbert and Steinitz, § Noether and Artin
- Hazewinkel 1994, pp. 73–74
- ^
- Grätzer 2008, p. vii
- Chang & Keisler 1990, p. 603
- Knoebel 2011, p. 5
- Hazewinkel 1994, pp. 74–75
- ^
- Hazewinkel 1994, pp. 74–75
- Kleiner 2007, p. 100
- Carlson 2024, § History of topology
- ^
- Hazewinkel 1994, pp. 74–75
- Weibel 1995, p. xi, 4
- ^
- Krömer 2007, p. 61
- Laos 1998, p. 100
- ^
- Hazewinkel 1994, pp. 74–75
- Pratt 2022, § 6. Free Algebras
- ^
- Houston 2004, p. 319
- Neri 2019, p. xii
- Lidl & Pilz 1997, pp. vii–viii
- ^
- Kleiner 2007, p. 100
- Pratt 2022, § 5. Algebraization of Mathematics
- Maddocks 2008, p. 130
- Pratt 2022, § 5. Algebraization of Mathematics
- Mancosu 1999, pp. 84–85
- ^
- Pratt 2022, § 1.4 Cartesian geometry, § 3. Universal Algebra
- Danilov 2006, p. 174
- ^
- Pratt 2022, § 5.1 Algebraic Geometry
- Danilov 2006, pp. 172, 174
- ^ Vince 2007, p. 133
- ^
- Pratt 2022, § 5.3 Algebraic Topology
- Rabadan & Blumberg 2019, pp. 49–50
- Nakahara 2018, p. 121
- Weisstein 2003, pp. 52–53
- ^
- Pratt 2022, § 5.2 Algebraic Number Theory
- Jarvis 2014, p. 1
- Viterbo & Hong 2011, p. 127
- ^
- ^
- Kilty & McAllister 2018, pp. x, 347, 589
- Bressoud 2021, p. 64
- ^
- Halmos 1956, p. 363
- Burris & Legris 2021, § 1. Introduction
- ^ Andréka, Németi & Sain 2001, pp. 133–134
- ^
- Andréka, Madarász & Németi 2020, § Concrete Algebraic Logic
- Pratt 2022, § 5.4 Algebraic Logic
- Plotkin 2012, pp. 155–156
- Jansana 2022, Lead section
- ^
- Andréka, Madarász & Németi 2020, § Abstract Algebraic Logic
- Jansana 2022, § 4. Algebras
- ^ Joyner 2008, p. 92
- ^
- Houston 2004, p. 319
- Neri 2019, p. xii
- Anton & Rorres 2010, p. 327
- ^
- Neri 2019, p. xii
- Aleskerov, Ersel & Piontkovski 2011, pp. 1–9
- Straffin 1980, p. 269
- Menini & Oystaeyen 2017, p. v
- Lovett 2015, p. ix
- Lidl & Pilz 1997, pp. vii–viii
- ^
- ^
- Klimov 2014, p. ix
- Bengtsson & Życzkowski 2017, pp. 313–353
- ^ Terras 2019, pp. 63–64, 142
- ^ Hull 2021, p. 180
- ^
- Lidl & Pilz 1997, pp. 183–184, 239–240
- Carstensen, Fine & Rosenberger 2011, pp. 326–327
- ^
- Kieran 2006, p. 15
- Kaput 2018, p. 186
- Gardella & DeLucia 2020, pp. 19–22
- ^
- Arcavi, Drijvers & Stacey 2016, p. xiii
- Dekker & Dolk 2011, p. 69
- ^
- ^
- Kieran 2006, p. 15
- Kaput 2018, p. 186
- Gardella & DeLucia 2020, pp. 19–22
- Star et al. 2015, pp. 16–17
- ^
- Arcavi, Drijvers & Stacey 2016, pp. 58–59
- Drijvers, Goddijn & Kindt 2011, p. 13
- ^ Hausberger, Zandieh & Fleischmann 2021, pp. 147–148
Sources
[edit]- Abas, Syed Jan; Salman, Amer Shaker (1994). Symmetries Of Islamic Geometrical Patterns. World Scientific. ISBN 978-981-4502-21-4. Retrieved March 12, 2024.
- Adhikari, Mahima Ranjan (2016). Basic Algebraic Topology and its Applications. Springer. ISBN 978-81-322-2843-1. Retrieved August 5, 2024.
- Adhikari, Mahima Ranjan; Adhikari, Avishek (2013). Basic Modern Algebra with Applications. Springer. ISBN 978-81-322-1599-8. Retrieved August 5, 2024.
- Aleskerov, Fuad; Ersel, Hasan; Piontkovski, Dmitri (2011). Linear Algebra for Economists. Springer. ISBN 978-3-642-20570-5. Retrieved March 11, 2024.
- Andréka, H.; Madarász, J. X.; Németi, I. (2020). "Algebraic Logic". Encyclopedia of Mathematics. Springer. Archived from the original on January 24, 2024. Retrieved October 23, 2023.
- Andréka, H.; Németi, I.; Sain, I. (2001). "Algebraic Logic". Handbook of Philosophical Logic. Springer. doi:10.1007/978-94-017-0452-6_3. ISBN 978-94-017-0452-6. Archived from the original on January 24, 2024. Retrieved January 24, 2024.
- Anton, Howard (2013). Elementary Linear Algebra. John Wiley & Sons. ISBN 978-1-118-67730-8. Retrieved January 18, 2024.
- Anton, Howard; Rorres, Chris (2010). Elementary Linear Algebra: Applications Version. John Wiley & Sons. ISBN 978-0-470-43205-1.
- Anton, Howard; Rorres, Chris (2013). Elementary Linear Algebra: Applications Version. John Wiley & Sons. ISBN 978-1-118-47422-8. Retrieved January 18, 2024.
- Arcavi, Abraham; Drijvers, Paul; Stacey, Kaye (2016). The Learning and Teaching of Algebra: Ideas, Insights and Activities. Routledge. ISBN 978-1-134-82077-1. Retrieved January 24, 2024.
- Artamonov, V. A. (2003). "Quasivarieties". In Hazewinkel, M. (ed.). Handbook of Algebra. Elsevier. ISBN 978-0-08-053297-4. Retrieved January 21, 2024.
- Atanasiu, Dragu; Mikusinski, Piotr (2019). A Bridge To Linear Algebra. World Scientific. ISBN 978-981-12-0024-3. Retrieved March 12, 2024.
- Bahturin, Y. (2013). Basic Structures of Modern Algebra. Springer. ISBN 978-94-017-0839-5. Retrieved August 30, 2024.
- Baranovich, T. M. (2023). "Algebraic Operation". Encyclopedia of Mathematics. Springer. Archived from the original on August 23, 2023. Retrieved January 11, 2023.
- Barrera-Mora, Fernando (2023). Linear Algebra: A Minimal Polynomial Approach to Eigen Theory. Walter de Gruyter GmbH & Co KG. ISBN 978-3-11-113591-5. Retrieved January 18, 2024.
- Bengtsson, Ingemar; Życzkowski, Karol (2017). Geometry of Quantum States: An Introduction to Quantum Entanglement (2nd ed.). Cambridge University Press. ISBN 978-1-107-02625-4.
- Benson, Donald C. (2003). A Smoother Pebble: Mathematical Explorations. Oxford University Press. ISBN 978-0-19-514436-9. Retrieved January 16, 2024.
- Berggren, John L. (2015). "Elementary Algebra". Encyclopædia Britannica. Archived from the original on January 14, 2024. Retrieved January 14, 2024.
- Betten, Anton; Kohnert, Axel; Laue, Reinhard; Wassermann, Alfred, eds. (2013). Algebraic Combinatorics and Applications. Springer. ISBN 978-3-642-59448-9.
- Bhattacharya, P. B.; Jain, S. K.; Nagpaul, S. R. (1994). Basic Abstract Algebra. Cambridge University Press. ISBN 978-0-521-46629-5.
- Borceux, Francis (1994). Handbook of Categorical Algebra: Basic category theory. Cambridge University Press. ISBN 978-0-521-44178-0.
- Bourbaki, N. (1998). Algebra I: Chapters 1-3. Springer. ISBN 978-3-540-64243-5.
- Boyer, Carl B.; Merzbach, Uta C. (2011). A History of Mathematics. John Wiley & Sons. ISBN 978-0-470-63056-3. Retrieved January 27, 2024.
- Bracken, Laura J.; Miller, Edward S. (2014). Elementary Algebra. Cengage Learning. ISBN 978-0-618-95134-5.
- Bressoud, David M. (2021). Calculus Reordered: A History of the Big Ideas. Princeton University Press. ISBN 978-0-691-21878-6. Retrieved September 4, 2024.
- Brezinski, Claude; Meurant, Gérard; Redivo-Zaglia, Michela (2022). A Journey through the History of Numerical Linear Algebra. SIAM. ISBN 978-1-61197-723-3. Retrieved August 12, 2024.
- Brešar, Matej (2014). Introduction to Noncommutative Algebra. Springer. ISBN 978-3-319-08693-4. Retrieved June 14, 2024.
- Brown, Jonathon D. (2015). Linear Models in Matrix Form: A Hands-On Approach for the Behavioral Sciences. Springer. ISBN 978-3-319-11734-8.
- Bueno, Otávio; French, Steven (2018). Applying Mathematics: Immersion, Inference, Interpretation. Oxford University Press. ISBN 978-0-19-881504-4. Retrieved July 28, 2024.
- Bukhshtab, A. A.; Pechaev, V. I. (2020). "Arithmetic". Encyclopedia of Mathematics. Springer. Archived from the original on October 4, 2009. Retrieved October 23, 2023.
- Burgin, Mark (2022). Trilogy Of Numbers And Arithmetic – Book 1: History Of Numbers And Arithmetic: An Information Perspective. World Scientific. ISBN 978-981-12-3685-3. Retrieved January 13, 2024.
- Burris, Stanley; Legris, Javier (2021). "The Algebra of Logic Tradition". The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. Archived from the original on January 29, 2024. Retrieved January 22, 2024.
- Carlson, Stephan C. (2024). "Topology – Homology, Cohomology, Manifolds". Encyclopædia Britannica. Retrieved October 2, 2024.
- Carstensen, Celine; Fine, Benjamin; Rosenberger, Gerhard (2011). Abstract Algebra: Applications to Galois Theory, Algebraic Geometry, and Cryptography. Walter de Gruyter. ISBN 978-3-11-025008-4.
- Chahal, J. S. (2018). Fundamentals of Linear Algebra. CRC Press. ISBN 978-0-429-75810-2. Retrieved August 29, 2024.
- Chang, C. C.; Keisler, H. J. (1990). Model Theory. Elsevier. ISBN 978-0-08-088007-5. Retrieved January 27, 2024.
- Cheng, Eugenia (2023). The Joy of Abstraction. Cambridge University Press. doi:10.1017/9781108769389. ISBN 978-1-108-47722-2.
- Christianidis, Jean; Megremi, Athanasia (2019). "Tracing the Early History of Algebra: Testimonies on Diophantus in the Greek-speaking World (4th–7th Century CE)". Historia Mathematica. 47: 16–38. doi:10.1016/j.hm.2019.02.002.
- Cohn, P. M. (1995). Skew Fields: Theory of General Division Rings. Cambridge University Press. ISBN 978-0-521-43217-7.
- Cohn, P. M. (2012). Universal Algebra. Springer. ISBN 978-94-009-8399-1. Retrieved June 14, 2024.
- Cooper, Ellis D. (2011). Mathematical Mechanics: From Particle to Muscle. World Scientific. ISBN 978-981-4289-70-2. Retrieved January 20, 2024.
- Corry, Leo (2024). "Algebra". Encyclopædia Britannica. Archived from the original on January 19, 2024. Retrieved January 25, 2024.
- Cox, David A. (2012). Galois Theory. John Wiley & Sons. ISBN 978-1-118-21842-6.
- Cresswell, Julia (2010). Oxford Dictionary of Word Origins. Oxford University Press. ISBN 978-0-19-954793-7. Retrieved January 27, 2024.
- Danilov, V. I. (2006). "II. Algebraic Varieties and Schemes". Algebraic Geometry I: Algebraic Curves, Algebraic Manifolds and Schemes. Springer. ISBN 978-3-540-51995-9. Retrieved January 24, 2024.
- Dekker, Truus; Dolk, Maarten (2011). "3. From Arithmetic to Algebra". In Drijvers, Paul (ed.). Secondary Algebra Education: Revisiting Topics and Themes and Exploring the Unknown. Springer. ISBN 978-94-6091-334-1. Retrieved January 24, 2024.
- Denecke, Klaus; Wismath, Shelly L. (2018). Universal Algebra and Applications in Theoretical Computer Science. CRC Press. ISBN 978-1-4822-8583-3. Retrieved August 30, 2024.
- Deo, Satya (2018). Algebraic Topology: A Primer. Springer. ISBN 978-981-10-8734-9. Retrieved August 5, 2024.
- Derbyshire, John (2006). "2. The Father of Algebra". Unknown Quantity: A Real and Imaginary History of Algebra. National Academies Press. ISBN 978-0-309-09657-7. Retrieved January 27, 2024.
- Dominich, Sándor (2008). The Modern Algebra of Information Retrieval. Springer. ISBN 978-3-540-77659-8. Retrieved January 20, 2024.
- Drijvers, Paul; Goddijn, Aad; Kindt, Martin (2011). "1. Algebra Education: Exploring Topics and Themes". In Drijvers, Paul (ed.). Secondary Algebra Education: Revisiting Topics and Themes and Exploring the Unknown. Springer. ISBN 978-94-6091-334-1. Retrieved January 24, 2024.
- Efimov, B. A. (2014). "Set theory". Encyclopedia of Mathematics. Springer. Archived from the original on November 29, 2022. Retrieved January 11, 2023.
- Elwes, Richard (December 2006). "An enormous theorem: the classification of finite simple groups". Plus Magazine. Archived from the original on February 2, 2009. Retrieved December 20, 2011.
- Emch, Gerard G.; Sridharan, R.; Srinivas, M. D. (2005). Contributions to the History of Indian Mathematics. Springer. ISBN 978-93-86279-25-5. Retrieved January 27, 2024.
- EoM Staff (2017). "Algebra". Encyclopedia of Mathematics. Springer. Archived from the original on November 29, 2022. Retrieved January 11, 2023.
- Fiche, Georges; Hebuterne, Gerard (2013). Mathematics for Engineers. John Wiley & Sons. ISBN 978-1-118-62333-6. Retrieved January 13, 2024.
- Gallier, Jean H.; Quaintance, Jocelyn (2020). Linear Algebra And Optimization With Applications To Machine Learning – Volume Ii: Fundamentals Of Optimization Theory With Applications To Machine Learning. World Scientific. ISBN 978-981-12-1658-9.
- Gandz, Solomon (1926). "The Origin of the Term "Algebra"". The American Mathematical Monthly. 33 (9): 437–440. doi:10.2307/2299605. JSTOR 2299605.
- Gardella, Francis; DeLucia, Maria (2020). Algebra for the Middle Grades. IAP. ISBN 978-1-64113-847-5. Retrieved January 24, 2024.
- Geddes, Keith O.; Czapor, Stephen R.; Labahn, George (2007). Algorithms for Computer Algebra. Springer. ISBN 978-0-585-33247-5.
- Gilbert, William J.; Nicholson, W. Keith (2004). Modern Algebra with Applications. John Wiley & Sons. ISBN 978-0-471-46989-6. Retrieved January 13, 2024.
- Godsil, Chris (2017). Algebraic Combinatorics. Routledge. ISBN 978-1-351-46750-6.
- Golan, Jonathan S. (1995). "Algebras Over A Field". Foundations of Linear Algebra. Kluwer Texts in the Mathematical Sciences. Vol. 11. Springer. pp. 219–227. doi:10.1007/978-94-015-8502-6_18. ISBN 978-94-015-8502-6. Archived from the original on January 12, 2024. Retrieved January 13, 2024.
- Goodman, A. W. (2001). Algebra From A To Z. Vol. 1. World Scientific. ISBN 978-981-310-266-8. Retrieved March 11, 2024.
- Gowers, Timothy; Barrow-Green, June; Leader, Imre, eds. (2010). The Princeton Companion to Mathematics. Princeton University Press. ISBN 978-1-4008-3039-8.
- Grätzer, George (2008). Universal Algebra (2 ed.). Springer. ISBN 978-0-387-77487-9. Retrieved January 27, 2024.
- Grillet, Pierre Antoine (2007). "Universal Algebra". Abstract Algebra. Graduate Texts in Mathematics. Vol. 242. Springer. pp. 559–580. doi:10.1007/978-0-387-71568-1_15. ISBN 978-0-387-71568-1. Archived from the original on January 12, 2024. Retrieved January 13, 2024.
- Häberle, L. (2009). "On Classification of Molecules and Species of Representation Rings". In Fink, Andreas; Lausen, Berthold; Seidel, Wilfried; Ultsch, Alfred (eds.). Advances in Data Analysis, Data Handling and Business Intelligence. Springer. ISBN 978-3-642-01044-6. Retrieved March 12, 2024.
- Halmos, Paul R. (1956). "The Basic Concepts of Algebraic Logic". The American Mathematical Monthly. 63 (6): 363–387. doi:10.2307/2309396. ISSN 0002-9890. JSTOR 2309396.
- Harrison, Michael; Waldron, Patrick (2011). Mathematics for Economics and Finance. Routledge. ISBN 978-1-136-81921-6. Retrieved January 18, 2024.
- Hausberger, Thomas (2020). "Abstract Algebra Teaching and Learning". In Lerman, Stephen (ed.). Encyclopedia of Mathematics Education (2 ed.). Springer. ISBN 9783030157883.
- Hausberger, Thomas; Zandieh, Michelle; Fleischmann, Yael (2021). "Abstract and Linear Algebra". In Durand-Guerrier, Viviane; Hochmuth, Reinhard; Nardi, Elena; Winsløw, Carl (eds.). Research and Development in University Mathematics Education: Overview Produced by the International Network for Didactic Research in University Mathematics. Routledge. ISBN 978-1-000-36924-3.
- Hazewinkel, Michiel (1994). Encyclopaedia of Mathematics (Set). Springer. ISBN 978-1-55608-010-4. Retrieved January 27, 2024.
- HC Staff (2022). "Arithmetic". American Heritage Dictionary. HarperCollins. Archived from the original on November 8, 2023. Retrieved October 19, 2023.
- Hettle, Cyrus (2015). "The Symbolic and Mathematical Influence of Diophantus's Arithmetica". Journal of Humanistic Mathematics. 5 (1): 139–166. doi:10.5642/jhummath.201501.08.
- Higgins, Peter M. (2015). Algebra: A Very Short Introduction. Oxford University Press. ISBN 978-0-19-104746-6. Retrieved January 27, 2024.
- Higham, Nicholas J. (2019). Handbook of Writing for the Mathematical Sciences (3 ed.). SIAM. ISBN 978-1-61197-610-6. Retrieved March 17, 2024.
- Hoad, T. F. (1993). The Concise Oxford Dictionary of English Etymology. Oxford University Press. ISBN 978-0-19-283098-2.
- Hohn, Franz E. (2013). Elementary Matrix Algebra. Dover Publications. ISBN 978-0-486-14372-9.
- Houston, Stephen D. (2004). The First Writing: Script Invention as History and Process. Cambridge University Press. ISBN 978-0-521-83861-0.
- Hull, Thomas C. (2021). Origametry: Mathematical Methods in Paper Folding. Cambridge University Press. ISBN 978-1-108-47872-4. Retrieved August 7, 2024.
- Igarashi, Yoshihide; Altman, Tom; Funada, Mariko; Kamiyama, Barbara (2014). Computing: A Historical and Technical Perspective. CRC Press. ISBN 978-1-4822-2741-3. Retrieved January 29, 2024.
- Indurkhya, Bipin (2013). "6.5 Algebras and Structures". Metaphor and Cognition: An Interactionist Approach. Springer. ISBN 978-94-017-2252-0. Retrieved January 21, 2024.
- Irving, Ronald S. (2004). Integers, Polynomials, and Rings: A Course in Algebra. Springer. ISBN 978-0-387-40397-7. Retrieved January 20, 2024.
- Ivanova, O. A.; Smirnov, D. M. (2012). "Isomorphism". Encyclopedia of Mathematics. Springer. Archived from the original on August 6, 2024. Retrieved March 11, 2024.
- Jansana, Ramon (2022). "Algebraic Propositional Logic". The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. Archived from the original on December 20, 2016. Retrieved January 22, 2024.
- Jarvis, Frazer (2014). Algebraic Number Theory. Springer. ISBN 978-3-319-07545-7. Retrieved January 24, 2024.
- Jenkins, Everett (2010). The Muslim Diaspora (Volume 1, 570-1500): A Comprehensive Chronology of the Spread of Islam in Asia, Africa, Europe and the Americas. McFarland. ISBN 978-0-7864-4713-8. Retrieved January 28, 2024.
- Joyner, David (2008). Adventures in Group Theory: Rubik's Cube, Merlin's Machine, and Other Mathematical Toys (2 ed.). Johns Hopkins University Press. ISBN 978-0-8018-9012-3.
- Kaput, James J. (2018). "Linking Representations in the Symbol Systems of Algebra". In Wagner, Sigrid; Kieran, Carolyn (eds.). Research Issues in the Learning and Teaching of Algebra: the Research Agenda for Mathematics Education, Volume 4. Routledge. ISBN 978-1-135-43414-4. Retrieved August 8, 2024.
- Kargapolov, M. I.; Merzlyakov, Yu. I. (2016). "Group". Encyclopedia of Mathematics. Springer. Archived from the original on December 5, 2022. Retrieved January 11, 2023.
- Karpilovsky, G. (1989). Topics in Field Theory. Elsevier. ISBN 978-0-08-087266-7.
- Kaufmann, Jerome E.; Schwitters, Karen L. (2011). Elementary Algebra. Cengage Learning. ISBN 978-1-4390-4917-4.
- Khattar, Dinesh; Agrawal, Neha (2023). Group Theory. Springer and Ane Books Pvt. Ltd. ISBN 978-3-031-21307-6. Retrieved January 20, 2024.
- Kieran, Carolyn (2006). "Research on the Learning and Teaching of Algebra". In Gutiérrez, Angel; Boero, Paolo (eds.). Handbook of Research on the Psychology of Mathematics Education: Past, Present and Future. Sense Publishers. ISBN 978-90-77874-19-6. Retrieved August 8, 2024.
- Kilty, Joel; McAllister, Alex (2018). Mathematical Modeling and Applied Calculus. Oxford University Press. ISBN 978-0-19-255813-8. Retrieved January 24, 2024.
- Kleiner, Israel (2007). A History of Abstract Algebra. Springer. ISBN 978-0-8176-4685-1.
- Klimov, D. M. (2014). Group-Theoretic Methods in Mechanics and Applied Mathematics. CRC Press. ISBN 978-1-4822-6522-4.
- Kline, Morris (1990). Mathematical Thought From Ancient to Modern Times: Volume 3. Oxford University Press. ISBN 978-0-19-506137-6.
- Knoebel, Arthur (2011). Sheaves of Algebras Over Boolean Spaces. Springer. ISBN 978-0-8176-4218-1. Retrieved January 27, 2024.
- Kramer, Jürg; Pippich, Anna-Maria von (2017). From Natural Numbers to Quaternions. Springer. ISBN 978-3-319-69429-0. Retrieved January 20, 2024.
- Krömer, Ralph (2007). Tool and Object: A History and Philosophy of Category Theory. Springer. ISBN 978-3-7643-7524-9.
- Kvasz, L. (2006). "The History of Algebra and the Development of the Form of Its Language". Philosophia Mathematica. 14 (3): 287–317. doi:10.1093/philmat/nkj017. ISSN 1744-6406.
- Lal, Ramji (2017). Algebra 2: Linear Algebra, Galois Theory, Representation Theory, Group Extensions and Schur Multiplier. Springer. ISBN 978-981-10-4256-0.
- Lamagna, Edmund A. (2019). Computer Algebra: Concepts and Techniques. CRC Press. ISBN 978-1-351-60583-0. Retrieved January 16, 2024.
- Lang, Serge (2005). Algebra. Springer. ISBN 978-0-387-95385-4.
- Laos, Nicolas K. (1998). Topics in Mathematical Analysis and Differential Geometry. World Scientific. ISBN 978-981-02-3180-4.
- Library of Congress. Library of Congress Classification: Class Q - Science (PDF). Library of Congress. Archived (PDF) from the original on April 5, 2024. Retrieved March 17, 2024.
- Lidl, Rudolf; Pilz, Günter (1997). Applied Abstract Algebra. Springer. ISBN 978-0-387-98290-8.
- Lovett, Stephen (2015). Abstract Algebra: Structures and Applications. CRC Press. ISBN 978-1-4822-4891-3. Retrieved July 27, 2024.
- Lukas, Andre (2022). The Oxford Linear Algebra for Scientists. Oxford University Press. ISBN 978-0-19-258347-5.
- Maddocks, J. R. (2008). "Algebra". In Lerner, Brenda Wilmoth; Lerner, K. Lee (eds.). The Gale Encyclopedia of Science (4th ed.). Thompson Gale. ISBN 978-1-4144-2877-2. Archived from the original on January 12, 2024. Retrieved January 13, 2024.
- Majewski, Miroslaw (2004). MuPAD Pro Computing Essentials (2 ed.). Springer. ISBN 978-3-540-21943-9.
- Mal’cev, A. I. (1973). "Quasivarieties". Algebraic Systems. Springer. pp. 210–266. doi:10.1007/978-3-642-65374-2_5. ISBN 978-3-642-65374-2. Archived from the original on June 18, 2018. Retrieved January 21, 2024.
- Mancosu, Paolo (1999). Philosophy of Mathematics and Mathematical Practice in the Seventeenth Century. Oxford University Press. ISBN 978-0-19-513244-1. Retrieved January 24, 2024.
- Markushevich, A. I. (2015). "Polynomial". Encyclopedia of Mathematics. Springer. Archived from the original on August 6, 2024. Retrieved January 11, 2023.
- Maxwell, E. A. (2009). Algebraic Structure and Matrices Book 2. Syracuse University Press. ISBN 978-0-521-10905-5. Retrieved January 20, 2024.
- McKeague, Charles P. (1986). Elementary Algebra. Academic Press. ISBN 978-1-4832-6384-7.
- McKeague, Charles P. (2014). Intermediate Algebra: A Text/Workbook. Academic Press. ISBN 978-1-4832-1417-7. Retrieved January 16, 2024.
- McWeeny, R. (2002). Symmetry: An Introduction to Group Theory and Its Applications. Courier Corporation. ISBN 978-0-486-42182-7. Retrieved January 20, 2024.
- Menini, Claudia; Oystaeyen, Freddy Van (2017). Abstract Algebra: A Comprehensive Treatment. CRC Press. ISBN 978-1-4822-5817-2. Retrieved January 27, 2024.
- Merzlyakov, Yu. I.; Shirshov, A. I. (2020). "Algebra(2)". Encyclopedia of Mathematics. Springer. Archived from the original on April 7, 2023. Retrieved January 11, 2023.
- Mirakhor, Abbas; Krichene, Noureddine (2014). Introductory Mathematics and Statistics for Islamic Finance. John Wiley & Sons. ISBN 978-1-118-77972-9. Retrieved August 7, 2024.
- Mishra, Sanjay (2016). Fundamentals of Mathematics: Algebra. Pearson India. ISBN 978-93-325-5891-5.
- Miyake, Katsuya (2002). "Some Aspects on Interactions between Algebraic Number Theory and Analytic Number Theory". In Kanemitsu, Shigeru; Jia, Chaohua (eds.). Number Theoretic Methods: Future Trends. Springer. ISBN 978-1-4419-5239-4. Retrieved August 7, 2024.
- Mortensen, C. E. (2013). Inconsistent Mathematics. Springer. ISBN 978-94-015-8453-1. Retrieved January 18, 2024.
- Murthy, Swamy and (2012). Algebra: Abstract and Modern. Pearson Education India. ISBN 978-93-325-0993-1. Retrieved August 5, 2024.
- Musser, Gary L.; Peterson, Blake E.; Burger, William F. (2013). Mathematics for Elementary Teachers: A Contemporary Approach. John Wiley & Sons. ISBN 978-1-118-48700-6. Retrieved March 11, 2024.
- MW Staff (2023). "Definition of Arithmetic". Merriam-Webster. Archived from the original on November 14, 2023. Retrieved October 19, 2023.
- Nakahara, Mikio (2018). Geometry, Topology and Physics. Taylor & Francis. ISBN 978-1-4200-5694-5. Retrieved January 24, 2024.
- Neri, Ferrante (2019). Linear Algebra for Computational Sciences and Engineering. Springer. ISBN 978-3-030-21321-3. Retrieved January 24, 2024.
- Nicholson, W. Keith (2012). Introduction to Abstract Algebra. John Wiley & Sons. ISBN 978-1-118-13535-8. Retrieved August 30, 2024.
- Oaks, Jeffrey A.; Alkhateeb, Haitham M. (2007). "Simplifying equations in Arabic algebra". Historia Mathematica. 34 (1): 45–61. doi:10.1016/j.hm.2006.02.006.
- Olver, Peter J. (1999). Classical Invariant Theory. Cambridge University Press. ISBN 978-0-521-55821-1. Retrieved March 12, 2024.
- Ono, Hiroakira (2019). Proof Theory and Algebra in Logic. Springer. ISBN 978-981-13-7997-0.
- OUP Staff. "Algebra". Lexico. Oxford University Press. Archived from the original on November 20, 2013.
- Ovchinnikov, Sergei (2015). Number Systems. American Mathematical Society. ISBN 978-1-4704-2018-5. Retrieved January 20, 2024.
- Pickover, Clifford A. (2009). The Math Book: From Pythagoras to the 57th Dimension, 250 Milestones in the History of Mathematics. Sterling Publishing Company, Inc. ISBN 978-1-4027-5796-9. Retrieved January 28, 2024.
- Plotkin, B. (2012). Universal Algebra, Algebraic Logic, and Databases. Springer. ISBN 978-94-011-0820-1. Retrieved January 24, 2024.
- Pratt, Vaughan (2022). "Algebra". The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. Archived from the original on January 29, 2024. Retrieved January 11, 2024.
- Rabadan, Raul; Blumberg, Andrew J. (2019). Topological Data Analysis for Genomics and Evolution: Topology in Biology. Cambridge University Press. ISBN 978-1-107-15954-9. Retrieved January 24, 2024.
- Ricardo, Henry (2009). A Modern Introduction to Linear Algebra. CRC Press. ISBN 978-1-4398-9461-3. Retrieved August 29, 2024.
- Rohde, Ulrich L.; Jain, G. C.; Poddar, Ajay K.; Ghosh, A. K. (2012). Introduction to Differential Calculus: Systematic Studies with Engineering Applications for Beginners. John Wiley & Sons. ISBN 978-1-118-13014-8. Retrieved January 16, 2024.
- Romanowski, Perry (2008). "Arithmetic". In Lerner, Brenda Wilmoth; Lerner, K. Lee (eds.). The Gale Encyclopedia of Science (4th ed.). Thompson Gale. ISBN 978-1-4144-2877-2. Archived from the original on November 1, 2023. Retrieved January 13, 2024.
- Rosen, Kenneth (2012). Discrete Maths and Its Applications Global Edition 7e. McGraw Hill. ISBN 978-0-07-715151-5.
- Rowen, Louis Halle (2006). Graduate Algebra: Commutative View: Commutative View. American Mathematical Society. ISBN 978-0-8218-0570-1. Retrieved June 14, 2024.
- Sahai, Vivek; Bist, Vikas (2002). Linear Algebra. CRC Press. ISBN 978-0-8493-2426-0.
- Saikia, Promode Kumar (2008). Linear Algebra. Pearson Education India. ISBN 978-81-317-4276-1. Retrieved August 5, 2024.
- Serovajsky, Simon (2020). Architecture of Mathematics. CRC Press. ISBN 978-0-429-89353-7.
- Seshadri, C. S. (2010). Studies in the History of Indian Mathematics. Springer. ISBN 978-93-86279-49-1. Retrieved January 27, 2024.
- Sialaros, Michalis (2018). Revolutions and Continuity in Greek Mathematics. Walter de Gruyter GmbH & Co KG. ISBN 978-3-11-056527-0. Retrieved January 27, 2024.
- Silverman, Joseph H. (2022). Abstract Algebra: An Integrated Approach. American Mathematical Society. ISBN 978-1-4704-6860-6.
- Smirnov, D. M. (2020). "Universal Algebra". Encyclopedia of Mathematics. Springer. Archived from the original on March 1, 2024. Retrieved August 30, 2024.
- Smith, Jonathan D. H. (2015). Introduction to Abstract Algebra. CRC Press. ISBN 978-1-4987-3162-1. Retrieved June 14, 2024.
- Smorynski, Craig (2007). History of Mathematics: A Supplement. Springer. ISBN 978-0-387-75481-9. Retrieved January 27, 2024.
- Sneyd, James; Fewster, Rachel M.; McGillivray, Duncan (2022). Mathematics and Statistics for Science. Springer. ISBN 978-3-031-05318-4.
- Sobolev, S. K. (2015). "Constant". Encyclopedia of Mathematics. Springer. Archived from the original on January 24, 2024. Retrieved October 23, 2023.
- Solomon, Bruce (2014). Linear Algebra, Geometry and Transformation. CRC Press. ISBN 978-1-4822-9930-4. Retrieved August 29, 2024.
- Sorell, Tom (2000). Descartes: A Very Short Introduction. Oxford University Press. ISBN 978-0-19-285409-4. Retrieved March 11, 2024.
- Star, Jon R.; Foegen, Anne; Larson, Matthew R.; McCallum, William G.; Porath, Jane; Zbiek, Rose Mary (2015). Teaching Strategies for Improving Algebra Knowledge in Middle and High School Students. U.S. Department of Education / Institute of Education Sciences. OCLC 5867417164.
- Straffin, Philip D. (1980). "Linear Algebra in Geography: Eigenvectors of Networks". Mathematics Magazine. 53 (5): 269–276. doi:10.2307/2689388. ISSN 0025-570X. JSTOR 2689388.
- Sullivan, Michael (2010). Finite Mathematics: An Applied Approach. John Wiley & Sons. ISBN 978-0-470-87639-8. Retrieved January 18, 2024.
- Tan, Kiat Shi; Steeb, Willi-Hans; Hardy, Yorick (2012). SymbolicC++:An Introduction to Computer Algebra Using Object-Oriented Programming: An Introduction to Computer Algebra Using Object-Oriented Programming. Springer. ISBN 978-1-4471-0405-6. Retrieved January 16, 2024.
- Tanton, James (2005). Encyclopedia of Mathematics. Facts On File. ISBN 978-0-8160-5124-3.
- Terras, Audrey (2019). Abstract Algebra with Applications. Cambridge University Press. ISBN 978-1-107-16407-9.
- Tsokos, Chris P.; Wooten, Rebecca D. (2015). The Joy of Finite Mathematics: The Language and Art of Math. Academic Press. ISBN 978-0-12-802985-5.
- Valenza, Robert J. (2012). Linear Algebra: An Introduction to Abstract Mathematics. Springer. ISBN 978-1-4612-0901-0. Retrieved August 29, 2024.
- Vince, John (2007). Vector Analysis for Computer Graphics. Springer. ISBN 978-1-84628-803-6. Retrieved August 5, 2024.
- Viterbo, Emanuele; Hong, Yi (2011). "3.4 Algebraic Number Theory". In Hlawatsch, Franz; Matz, Gerald (eds.). Wireless Communications Over Rapidly Time-Varying Channels. Academic Press. ISBN 978-0-08-092272-0. Retrieved January 24, 2024.
- Voitsekhovskii, M. I. (2011). "Linear Equation". Encyclopedia of Mathematics. Springer. Archived from the original on November 23, 2023. Retrieved January 10, 2024.
- Waerden, Bartel L. van der (2003). Algebra. Vol. 1. Springer. ISBN 0-387-40624-7.
- Waerden, Bartel L. van der (2013). A History of Algebra: From al-Khwārizmī to Emmy Noether. Springer. ISBN 978-3-642-51599-6. Retrieved January 27, 2024.
- Wagner, Sigrid; Kieran, Carolyn (2018). Research Issues in the Learning and Teaching of Algebra: The Research Agenda for Mathematics Education. Vol. 4. Routledge. ISBN 978-1-135-43421-2. Retrieved January 13, 2024.
- Walz, Guido (2016). "Algebra". Lexikon der Mathematik: Band 1: A bis Eif [Encyclopedia of Mathematics: Volume 1: A to Eif] (in German). Springer. ISBN 978-3-662-53498-4. Archived from the original on January 12, 2024. Retrieved January 13, 2024.
- Weibel, Charles A. (1995). An Introduction to Homological Algebra. Cambridge University Press. ISBN 978-1-139-64307-8.
- Weisstein, Eric W. (2003). CRC Concise Encyclopedia of Mathematics (2nd ed.). Chapman & Hall/CRC. ISBN 978-1-58488-347-0.
- Wheeler, Jeffrey Paul (2023). An Introduction to Optimization with Applications in Machine Learning and Data Analytics. CRC Press. ISBN 978-1-003-80359-1.
- Whitelaw, T. A. (1995). Introduction to Abstract Algebra, Third Edition. CRC Press. ISBN 978-0-7514-0147-9.
- Williams, G. Arnell (2022). Algebra the Beautiful: An Ode to Math's Least-Loved Subject. Basic Books. ISBN 978-1-5416-0070-6. Retrieved March 11, 2024.
- Wilson, Robert A. (2009). The Finite Simple Groups. Graduate Texts in Mathematics. Vol. 251. Springer-Verlag. doi:10.1007/978-1-84800-988-2. ISBN 978-1-84800-987-5. Zbl 1203.20012.
- Young, Cynthia Y. (2010). Precalculus. John Wiley & Sons. ISBN 978-0-471-75684-2. Retrieved January 16, 2024.
- Young, Cynthia Y. (2023). Precalculus. John Wiley & Sons. ISBN 978-1-119-86940-5. Retrieved January 18, 2024.
- zbMATH Open (2024). "Classification". zbMATH Open. Mathematical Reviews and zbMATH Open. Archived from the original on July 19, 2020. Retrieved March 17, 2024.
- Zwillinger, Daniel (2002). CRC Standard Mathematical Tables and Formulae. CRC Press. ISBN 978-1-4200-3534-6. Retrieved January 27, 2024.
































































































