Talk:Circle of fifths
| This is the talk page for discussing improvements to the Circle of fifths article. This is not a forum for general discussion of the article's subject. |
Article policies
|
| Find sources: Google (books · news · scholar · free images · WP refs) · FENS · JSTOR · TWL |
| Archives: 1, 2Auto-archiving period: 12 months |
| This It is of interest to the following WikiProjects: | ||||||||||||||||||
| ||||||||||||||||||
Circle of fifths in quarter tones?
[edit]DASL51984 added in the lead of this article that "some tunings, such as quarter tones, have multiple such circles." This is rather puzzling. First "quarter tones" is not a tuning. Let's assume that what is meant is a tuning producing 24 (equal or unequal) degrees in the octave. I fail to see, however, how a circle or pure fifths could produce a series of 24 degrees and I don't understand what "multiple cicles" means. There are two possibilities:
- One is to consider that a spiral of fifths (because our "circle" is a spiral in any tuning other than equal), if extended far enough, would produce quarter tones. But enharmonies are a comma apart, and a comma is about an 1/8-tone at most, so that the tuning would produce 48 degrees in the octave! I think to remember that Safi al-Din al-Urmawi, in the 13th century, had tried an extended Pythagorean tuning to describe the quarter tones of Arabic music, but eventually abandoned the idea. (This was discussed in a book by Liberty Manik, Das arabische Tonsystem im Mittelalter, which I don't have at hand just now.)
- Or DASL51984 is thinking of two circles of fiths, each of 12 degrees (or more with enharmonies) and a quarter tone apart. If that is what is meant, it should be better described, but I don't see the point of these two circles, and I never saw this in any theory of quarter tone music that I know.
There might of course be another explanation, of which I didn't think. — Hucbald.SaintAmand (talk) 16:02, 25 April 2024 (UTC)
- To a larger point - don't start out the description with rare cases and complicated exceptions. Non 12-tone tunings, keys with double sharps and flats - please, please no. This is what makes many WP articles unhelpful. - Special-T (talk) 16:34, 25 April 2024 (UTC)
- DASL51984 added an image of a "Circle of fifths in 19-tone equal temperament" that shows "enharmonies" that are not true enharmonies (for instance, C
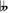 is not the enharmony of B, but of B♭). It is only because of these false enharmonies that the image can pretend to come to the octave or the unisson after 19 fifths – and/or these fifths cannot be true fifths. I fully agree with Special-T that the initial description should not deal with complicated exceptions, but here, in addition, I don't understand the "exception". — Hucbald.SaintAmand (talk) 13:54, 26 April 2024 (UTC)
is not the enharmony of B, but of B♭). It is only because of these false enharmonies that the image can pretend to come to the octave or the unisson after 19 fifths – and/or these fifths cannot be true fifths. I fully agree with Special-T that the initial description should not deal with complicated exceptions, but here, in addition, I don't understand the "exception". — Hucbald.SaintAmand (talk) 13:54, 26 April 2024 (UTC)
- The article 19_equal_temperament clearly states that in this case the cycle of fifths does not apply. One reads there: "repeating any fixed interval in this tuning system cycles through all possible notes, just as one may cycle through 12-EDO on the circle of fifths". This means that one may not cycle through 19-EDO on the same circle. I think that User:DASL51984 should reply. — Hucbald.SaintAmand (talk) 13:19, 27 April 2024 (UTC)
- DASL51984 added an image of a "Circle of fifths in 19-tone equal temperament" that shows "enharmonies" that are not true enharmonies (for instance, C
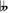 is not the enharmony of B, but of B♭). It is only because of these false enharmonies that the image can pretend to come to the octave or the unisson after 19 fifths – and/or these fifths cannot be true fifths
is not the enharmony of B, but of B♭). It is only because of these false enharmonies that the image can pretend to come to the octave or the unisson after 19 fifths – and/or these fifths cannot be true fifths
- DASL51984 added an image of a "Circle of fifths in 19-tone equal temperament" that shows "enharmonies" that are not true enharmonies (for instance, C
- The enharmonic equivalences in 19-tone equal temperament are different than those of 12-tone equal temperament. In 12-tone equal temperament, for example, C
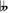 is equivalent to B♭, but in 19-tone equal temperament, C
is equivalent to B♭, but in 19-tone equal temperament, C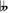 is equivalent to B natural. However, I think User:Special-T is right—their cases are best left to the dedicated articles, and in this article the fact that the circle of fifths is different in other tunings should just be hinted at, but it should be mentioned.
is equivalent to B natural. However, I think User:Special-T is right—their cases are best left to the dedicated articles, and in this article the fact that the circle of fifths is different in other tunings should just be hinted at, but it should be mentioned.
- The article 19_equal_temperament clearly states that in this case the cycle of fifths does not apply. One reads there: "repeating any fixed interval in this tuning system cycles through all possible notes, just as one may cycle through 12-EDO on the circle of fifths". This means that one may not cycle through 19-EDO on the same circle.
- I assume what you meant by this is "one may not cycle through 19-EDO using 12-EDO's circle of fifths." This is true, but one needs to remember that the cycle of fifths is not something that is specific to 12-tone equal temperament, nor is it something that must be limited to 12 pitches per octave. In any tuning where stacking the interval closest to 3/2 will cycle through all notes, the cycle of fifths applies. The statement "repeating any fixed interval in this tuning system cycles through all possible notes" implies that one may cycle through all notes of 19-EDO using its perfect fourth and fifth, just like in 12-TET. In 19-TET the circle of fifths is different than in 12-TET. DASL51984 (Speak to me!) 17:58, 27 April 2024 (UTC)
- The article 19_equal_temperament clearly states that in this case the cycle of fifths does not apply. One reads there: "repeating any fixed interval in this tuning system cycles through all possible notes, just as one may cycle through 12-EDO on the circle of fifths". This means that one may not cycle through 19-EDO on the same circle. I think that User:DASL51984 should reply. — Hucbald.SaintAmand (talk) 13:19, 27 April 2024 (UTC)
- Or DASL51984 is thinking of two circles of fiths, each of 12 degrees (or more with enharmonies) and a quarter tone apart. If that is what is meant, it should be better described, but I don't see the point of these two circles, and I never saw this in any theory of quarter tone music that I know.
- DASL51984 added an image of a "Circle of fifths in 19-tone equal temperament" that shows "enharmonies" that are not true enharmonies (for instance, C
- This was what I was getting at. In 24-tone equal temperament, for example, all the common notes are on one circle, but that only covers half of the notes. The half-sharps, half-flats, et cetera are on another circle and can't be reached using only fifths—tunings with multiple rings of fifths require the use of other generators. I recommend you check out Xenharmonic Wiki's article on ring number which describes this in more detail. DASL51984 (Speak to me!) 17:48, 27 April 2024 (UTC)
- This, for 24-tone ET, makes (some) sense, but needs further explanation in the article. I am perfectly aware of the Xhenarmonic website, but it should be refered to in the article and to its readers. One might imagine a separate section explaining how ETs with a multiple of 12 tones might be formed of parallel circles. I don't see the point, but I leave that up to you.
- I am more doubtful about 19-tone ET. Here, you cannot build parallel circles. I'd like to read a definition of what you understand by a "fifth" in that case. Strictly speaking, a fifth is an interval of five degrees in a diatonic scale. The definition may be extended to seven degrees in a chromatic scale, because this merely assumes the definition of "whole steps" and "half steps". You might argue that a "fifth" in any ET with more than 12 tones is the interval which comes closest to 702 cents, but that seems to me quite farfetched. First, in some tunings, there might be no interval close to 702 cents; and if you call a "fifth" the interval of 11 unit intervals (694,7 cents in 19-tone ET, 11 unit intervals or 12 degrees, if I am not mistaken), in what sense do you call that a "fifth", and why? Is there any interest in saying that 19-tone ET can approximately be formed by an approximate circle of "twelves" (rather than "fifths")?
- I don't mean that anything is this is wrong, but I think it would need a lot of explanation in an article titled "Circle of fifths", up to the point that I wonder whether all this really belongs there. One might add a section in an article on 19-tone ET explaining how the tuning can be built from a circle of something that might not necessarily be called a "fifth" – and also explaining why this may be of any interest. — Hucbald.SaintAmand (talk) 18:53, 27 April 2024 (UTC)
- Strictly speaking, a fifth is an interval of five degrees in a diatonic scale.
- A fifth is an interval of five degrees in any heptatonic MOS (moment of symmetry) scale. It's just safe to assume the main six modes of the diatonic scale in most of Western music.
- The definition may be extended to seven degrees in a chromatic scale, because this merely assumes the definition of "whole steps" and "half steps".
- There is a very good reason why I do not like using the terms "whole step" and "half step"—ther definitions are extremely narrow, and using them to describe the diatonic scale locks people into thinking in terms of only 12-TET, since fifths being exactly seven degrees in a chromatic scale is only true in 12-tone circulating temperaments. The diatonic scale itself is a very broad concept; C–D–E–F–G–A–B–C should not be thought as of strictly as "whole–whole–half–whole–whole–whole–half", but should thought of more generally, in terms of Long and Short intervals ("L–L–S–L–L–L–S").
- If the Long interval is 3 steps and the Short interval is 2 steps, we get 19-TET (1⁄3-comma meantone). Likewise, L = 5 and S = 3 gives us 31-TET (1⁄4-comma meantone), L = 7 and S = 4 gives 43-TET (1⁄5-comma meantone), L = 9 and S = 4 gives us 53-TET (Pythagorean tuning), and so on.
- You might argue that a "fifth" in any ET with more than 12 tones is the interval which comes closest to 702 cents, but that seems to me quite farfetched.
- Not really, since thinking of it as the interval that is closest to 3/2 allows people to understand that there is much more to heptatonic scales than the diatonic scale.
- First, in some tunings, there might be no interval close to [3/2]
- Correct. These may be flatter than 7-tone equal temperament, in which you'll get S–S–L–S–S–S–L– instead of L–L–S–L–L–L–S. The temperament that produces this "flipped" heptatonic scale is called "Mavila", but Mavila is outside the scope of this article.
- and if you call a "fifth" the interval of 11 unit intervals (694,7 cents in 19-tone ET, 11 unit intervals or 12 degrees, if I am not mistaken), in what sense do you call that a "fifth", and why? Is there any interest in saying that 19-tone ET can approximately be formed by an approximate circle of "twelves" (rather than "fifths")?
- Because C to G is still the fifth degree of the major scale, it's just that in 19-TET the whole tones (the Long intervals) are three steps instead of two, and the minor seconds (E–F and B–C, the Short intervals) are two steps instead of one. Again, think of the major scale in terms of Long/Short instead of Whole/Half.
- I don't mean that anything is this is wrong, but I think it would need a lot of explanation in an article titled "Circle of fifths", up to the point that I wonder whether all this really belongs there. One might add a section in an article on 19-tone ET explaining how the tuning can be built from a circle of something that might not necessarily be called a "fifth" – and also explaining why this may be of any interest.
- The main gripe I have is that the fact that the way most people and resources on the Internet explain the diatonic scale and its intervals is heavily biased in favour of 12-TET, when they should be using a more general approach. Going into more detail (not full-out regular temperament theory, but at least making sure that you're not telling people that one highly specific case is the only way to do things) is necessary if musicians are to have a complete understanding of how the things they're learning work. DASL51984 (Speak to me!) 21:13, 27 April 2024 (UTC)
- I won't continue arguing, I'll leave that to other readers of this article. One point, though. I am by profession a historian of music theory and I note that the idea of the semitone being half the tone (or the half step being half the whole step) is more than 2000 years old. It originated when the Ancient Greeks decided to call the semitone ημιτόνoς, hemitonos, meaning "the half of a tone". This somehow was an intuition of ET, millenia before it was clearly described. Music theory is a historical fact, I can understand your desire to generalize it, but one cannot go against history. — Hucbald.SaintAmand (talk) 07:14, 28 April 2024 (UTC)
- I didn't mean to come across as "I'm right, you're wrong", so I'm sorry if I did. I just wanted to make it clear that the concept itself is fundamentally broad (id est: this isn't something I came up with just for the sake of it), and the semitone being half of the tone is only one specific case out of many. DASL51984 (Speak to me!) 09:44, 28 April 2024 (UTC)
- Neither did I mean that we were entering a dispute, I only meant that the matter should not be discussed between us two, that other readers interested in this article should give their opinion. — Hucbald.SaintAmand (talk) 11:46, 29 April 2024 (UTC)
- I didn't mean to come across as "I'm right, you're wrong", so I'm sorry if I did. I just wanted to make it clear that the concept itself is fundamentally broad (id est: this isn't something I came up with just for the sake of it), and the semitone being half of the tone is only one specific case out of many. DASL51984 (Speak to me!) 09:44, 28 April 2024 (UTC)
- I won't continue arguing, I'll leave that to other readers of this article. One point, though. I am by profession a historian of music theory and I note that the idea of the semitone being half the tone (or the half step being half the whole step) is more than 2000 years old. It originated when the Ancient Greeks decided to call the semitone ημιτόνoς, hemitonos, meaning "the half of a tone". This somehow was an intuition of ET, millenia before it was clearly described. Music theory is a historical fact, I can understand your desire to generalize it, but one cannot go against history. — Hucbald.SaintAmand (talk) 07:14, 28 April 2024 (UTC)
I think it's safe to say that 17-TET (or 24-TET) is a WP:FRINGE topic, only experienced by a tiny minority of readers. Obviously not all music is 12-TET, but it represents the vast majority of music that most readers will have experienced, at least in Western countries (if non-Western countries use the idea of "circle of fifths," that's another matter). I don't have a problem with including how this concept applies to other tuning systems, as long as it's explained clearly (as Hucbald suggested) and meets WP:SOURCE, but it doesn't belong anywhere near the lede, per WP:DUE. —Wahoofive (talk) 15:42, 19 May 2024 (UTC)
- I'd add that one of the main problems I have with the description of cycles of fifths in systems with more than 12 degrees is the meaning of "enharmony". It should denote notes that sound the same despite different spellings (Webster). I fail to see how, say, Cbb could be enharmonic to B — or this corresponds to a musical notation that I don't know and that, so far as I have been able to discover, is not described in WP. And we need a clear definition of what a fifth is — to me, it is an interval of five steps in the system considered (or in a background system). — Hucbald.SaintAmand (talk) 19:28, 19 May 2024 (UTC)
- A detailed explanation of how C𝄫 could be enharmonic to B♮ (as is the case in 19-TET) would require discussing the details of meantone itself, since meantone is the basis of modern common-practice Western music theory, not 12-TET specifically, but that would be best left to the article on meantone, not here. DASL51984 (Speak to me!) 04:08, 20 May 2024 (UTC)
Umbilic torus gif
[edit]
This image recently showed up in the "Modulation and chord progression" section, without accompanying text to explain it or motivate its inclusion. What encyclopedic value does it add? Just plain Bill (talk) 12:32, 24 May 2024 (UTC)
- Hi,
- The already existed text fits perfectly to the gif file. I do not think it needs any addition. Text says
- "The circle of fifths is used to organize and describe the harmonic or tonal function of chords. Chords can progress in a pattern of ascending perfect fourths (alternately viewed as descending perfect fifths) in "functional succession".
- The image does exactly that. Watch out a fixed CEBG rectangular. It is a C major seventh. Or anyone can imagine it as just CEG, a major chord. This chord moves by ``ascending perfect fourth" to F major. Next by another ``ascending perfect fourth" to Bb major. And so on until, by three visual turns, cover the whole circle of fifths and comes to where it started (because circle of fifths is a circle). It is self-evident that the single path C-F-Bb-Eb-etc is the circle of fifths. Compare the notes with the above image counterclockwise.
- If the fact was not so self-evident, I would not dare to edit wikipedia. All sources that came to my attention recognize that there should exist a torus, like figure 5.9 on page 81 of pages's further reading or torus in Neo-Riemannian theory but can not clearly support the text ``Chords can progress in a pattern of ascending perfect fourths'' . The already existed text, however, can be supported perfectly, in a self-evident matter, by the C-F-Bb-Eb-etc curved path on the surface of an Umbilic torus.
- If anyone follows the details of my image can see, in another image, that in the gif contains the twelve tones, twelve minor and twelve major chords in a pattern of ascending perfect fourths but that would indeed need accompanying text and common agreement on the correspondences.
- The encyclopedic value of it is that the already existed text can be supported by a three-dimensional object and, in that knowledge, everyone would like to literally play the harmony of the 12 tone equal temperament system on their fingers.
- I am at your disposal for any further clarification Jimishol (talk) 15:00, 24 May 2024 (UTC)
- Thanks for these explanations. I nevertheless fail to see how this drawing can show a circle of fifths, nor how it can "organize and describe the harmonic or tonal function of chords." The text itself is not clear: it is not the chords themselves that "progress in a pattern of ascending perfect fourths," but their roots. What a "functional succession" is seems to me totally unclear (a succession of functions? But roots ain't functions!). The image shows a succession of identical chords (e.g. major sevenths), but no "functional succession" could be a succession of identical chords!!! Hucbald.SaintAmand (talk) 21:40, 25 May 2024 (UTC)
- From the definition in the article "The circle of fifths organizes pitches in a sequence of perfect fifths, generally shown as a circle..." it follows that it is a sequence of notes. They are usually shown as a closed curve of a circle in two-dimensional space. The definition is not violated if they are shown as a closed curve in three-dimensional space, as in the gif. On the contrary, the gif reinforces the definition that it is a sequence of notes, since, in the same article, there is a mapping of the sequence to some other curve than a circle.
- The title of our paragraph "Modulation and chord progression" and the explanatory text "Chord progressions also often move between chords whose roots are related by perfect fifth,...." already maps the notes of the sequence to chord roots. It is not the gif's responsibility to do so.
- Therefore the movement in the gif ...G-C-F... is, in the spirit of the paragraph, a major chord progression.
- The use of the phrase `Chords can progress ... in "functional succession"` implicitly assumes that a scale has been defined, otherwise "function" cannot be defined, in my opinion. Again, the gif doesn't need to clarify anything in favour of this.
- So I think it would be fair for the gif to have the same fate as the text it seems to support. To me, the gif is less ambiguous than the text it supports. In fact, I think the image better expresses what the text wants to communicate. The following explanation of functional succession, then, applies first to the text, then to the gif.
- By defining the C major as tonic then the movement of the example can be seen as...G-C-F...=...V-I-IV... In the figure a seventh major is moved to make it clearer that a scale can be visualized, in some way, as a surface. In the gif, the C major scale seems to create at least the "half cylinder" outlined by the movement of the BG edge to EC and finally to AF. As is natural, the repetition of the same perfect fourth movement changes scale (in the figure, surface) and therefore it takes three cycles to repeat the C major of the initial position, because we pass through all the scales. I am totally against considering chords as surfaces of triangles but in this case if you fold the tonnetz diagram over the surface of the gif you will see the V-iii-I-vi-IV motion. To stay in tonic we must return to tonic in only one rotation, not three as in the gif. The only way to use D while staying in scale is to use it as the vertex of the minor triangle DFA of the "top" surface and, from there to "slide" to the vertex D of the GBD major of the "bottom" surface. Thus the above functional succession becomes I-vi-IV-ii-V-iii-I and thus return to tonic with a single rotation.
- I don't think the paragraph should be inflated so as to lead the reader to specific mappings. These should be left to the opinions and perspective of each theorist or reader. But it seems that, for these mappings, I cannot avoid mentioning my own personal viewpoints, which are recorded in the link existed in the details of the image. I therefore prefer the mapping of each note to the vertices. The mapping of major scales or chords to a curved section starting from the homonymous vertex, e.g. C major to the CF curve. The mapping of minor scales or chords to a section of a straight line starting from the homonymous vertex, e.g. c minor to the CAb edge.
- Then, personally at least, I can even "see" the progress of the Neapolitan sixth through the path C-f-Db=CF-Fdb-DbF# From this perspective, the Fdb edge is the f minor, intermediate scale that does not need to be established, so with reference to it I have V-(i)-VI=V-VI of the f minor. By the same visualized logic, D major is Neapolitan of Db major, but because we must not use F# (leading tone of G) we compose and advance by a perfect fourth from D to G major. Visually at least, I can "see" the I-bII-V sequence, easily rather, somewhat like a "sequence" of two Neapolitans.
- The gif shows the sequence of perfect fourths on a three-dimensional closed curve, as an alternative way of representing the circle of fifths. It is not his responsibility to suggest the best possible mappings of the functional succession. But it does exist and, as the beginning of the paragraph states, can be "...used to organize and describe the harmonic or tonal function of chords..."
- Translated with DeepL.com (free version)
- I am at your disposal for any further clarification Jimishol (talk) 10:09, 26 May 2024 (UTC)
- Long story short. For each note, class [X], a local map is constructed containing the note [X] and its two basic connections to its "neighboring" notes [X*3/2] and [Y*5/4]. The set of twelve local maps, one for each note, defines a manifold as an abstract structure. But this structure can be viewed in three-dimensional space and visualized as in the gif. The four paths created by the branches [Y*5/4] are circles of sixths or the augmented triads. The unique path created by the branches [X*3/2] is the circle of fifths. So this is a mathematical-musical tool that can be used by any music theory (school), whether it wants to describe chord progressions or anything else. Jimishol (talk) 04:58, 28 May 2024 (UTC)
- I refer to manifold terminology because that's what I was familiar with. But I am puzzled by the fact that, when searching wikipedia, even in topological manifolds, their definition includes that they locally resemble real n-dimensional Euclidean space. To the question "is a tree graph a manifold with local maps the branches from each node?" the copilot answered "a tree graph exhibits manifold-like properties, especially when we focus on local regions around each node. It's a fascinating way to connect graph theory and geometry!". So a graph theory approach to gif might be more appropriate. Jimishol (talk) 08:38, 30 May 2024 (UTC)
- Long story short. For each note, class [X], a local map is constructed containing the note [X] and its two basic connections to its "neighboring" notes [X*3/2] and [Y*5/4]. The set of twelve local maps, one for each note, defines a manifold as an abstract structure. But this structure can be viewed in three-dimensional space and visualized as in the gif. The four paths created by the branches [Y*5/4] are circles of sixths or the augmented triads. The unique path created by the branches [X*3/2] is the circle of fifths. So this is a mathematical-musical tool that can be used by any music theory (school), whether it wants to describe chord progressions or anything else. Jimishol (talk) 04:58, 28 May 2024 (UTC)
- Thanks for these explanations. I nevertheless fail to see how this drawing can show a circle of fifths, nor how it can "organize and describe the harmonic or tonal function of chords." The text itself is not clear: it is not the chords themselves that "progress in a pattern of ascending perfect fourths," but their roots. What a "functional succession" is seems to me totally unclear (a succession of functions? But roots ain't functions!). The image shows a succession of identical chords (e.g. major sevenths), but no "functional succession" could be a succession of identical chords!!! Hucbald.SaintAmand (talk) 21:40, 25 May 2024 (UTC)
Chord progressions in the circle of fifths
[edit]The discussion in the section above (Talk:Circle of fifths#Umbilic torus gif) evolved into a discussion of chord progressions and their representation in the circle of fifths. User:Jimishol rigthly argues above that the image of the umbilic torus is not directly concerned by this discussion, that it might even be clearer than the text itself. I therefore open this new section to ask a few questions about Modulation and chord progression.
The text rightly begins saying that the circle of fifths illustrates the distance between keys, or between the roots of chords. But it continues stating that "The circle of fifths is used to organize and describe the harmonic or tonal function of chords" and refers to a website the purpose of which apparently is to propose (or, more precisely, to sell) "a songwriting tool" based on the "wheel of fifths". I am not sure that this is a valid source for Wikipedia, but let's leave the question aside for now.
I am not sure of what is meant by "organize" the function of chords. The text continues saying that chords can progress by fifths (or fourths) in what is called a "functional succession". But this in the sole occasion where this expression is used on WP. "Functional succcession" is found in Nattiez' Music and Discourse, quoted immediately after, where it apparently means "succession of functions" or, more precisely, succession of scale degrees – this is in a discussion of Wagner's "Tristan chord". The text continues commenting Nattiez (and Goldman, quoted by Nattiez) and concludes saying that in the succession I–IV–vii°–iii–vi–ii–V–I, IV is farther from I than ii. A reference to Simon Sechter would be welcome here, as all this is his "theory of the degrees".
To sum up, the problem is that the mention of "functions" in this context (i.e. in relation with the circle of fifths) is somewhat misleading. The website about the "wheel of thirds" truly considers harmonic functions and says that there are only three, T, S (or P) and D, which are not really described by the circle of fifths. The rest of the section calls "functions" what in reality is "degrees" (this seems to be common in American music theory) and discusses matters which do not really relate to the circle of fifths.
The section sould heavily be rewritten, in my opinion (or deleted, I am not sure it belongs to this article). Before working on it, however, I'd like to have the opinion of others. – Hucbald.SaintAmand (talk) 17:19, 26 May 2024 (UTC)
- When I first read the section, I had no problem understanding what it was trying to communicate. I think the text doesn't need radical changes and certainly not to disappear from wikipedia along with the gif. The phrase "functional succession" is in quotation marks generating skepticism that forces the reader to the immediately preceding link of Function (music). There we find that whichever terminology we choose to use depends on whether we are "followers" of German theory or Viennese theory. What I think the text is trying to say is that the sequence of notes of the cycle of fifths is a tool that can be used by all theories, each with its own terminology, because the 1:3/2 relation is objectively one of the most basic. Just because, in the discussion of the gif, the answer by necessity led to the mention of progressions with Roman numerals does not mean the gif or the text is necessarily connected to Viennese theory. Just from my perspective I happened to read Schoenberg. The fact that note names are used rather than Roman numerals or "functions" neutralizes both the text and the gif. In addition to the text, in the gif appears that the basic 1:3/2 relationship can be combined with the 1:5/4 of augmented triads to produce a coherent and simple result that can be visualized. I think Schoenberg would have happily wanted to use the gif image. But so would Riemann. Each in his own terminology.
- In conclusion, I think that perhaps all the text needs is for the phrase "Chords can progress in a pattern of ascending perfect fourths (alternately viewed as descending perfect fifths) in "functional succession"" to be extended to "Chords can progress in a pattern of ascending perfect fourths (alternately viewed as descending perfect fifths) in "functional succession", with the terminology depending on the theory that uses it."
- Translated with DeepL.com (free version) Jimishol (talk) 07:53, 27 May 2024 (UTC)
- What I feel problematic in the section is the confusion between German and Viennese theories. The first reference given is to Rogier Broekhuis' website and his "wheel of fifths", which probably uses the German (i.e. Riemann's) theory of functions. The problem is that this theory is not based on the cicle of fifths, as the three functions, T, S (or P) and D, are not necessarily a fifth (or a fourth) apart. Our text then turns to Nattiez' Music and Discourse which, in the English version particularly, is based on the Viennese theory (i.e. Sechter's theory of the degrees). (Nattiez' Musicologie générale et sémiologie is quite different from its translation; nothing like "functional succession" is found in the French version. I don't know whether this is because of changes made by Nattiez himself or by his translators.).
- So, the circle of fifths could be a tool, as you say, for the theory of the degrees (which is a theory of roots, as in Rameau's fundamental bass), but certainly not for the theory of (Riemannian) functions properly speaking – Dahlhaus, if I remember well, wrote about the difficulty of determining which degree primarily represents each function in Riemann's theory. I am perfectly aware that this confusion between German and Viennese theory exists in American theory today, but I see no reason to import it here, while it could almost completely be removed by replacing "function" by "degree" – and probably adding references to Rameau's fundamental bass and to Sechter's Grundsätze.
- And the statement that concludes the section, about the use of upper-case or lower-case Roman numerals, is totally irrelevant, as I–IV–VII–III–VI–II–V–I would make as much (or as little) sense as I–IV–vii°–iii–vi–ii–V–I, considering that, in a major scale, neither IV–VII nor IV–vii° is a pure fifth. Sechter's presentation of this series was VII–III–VI–II–V–I–IV. It is impossible to start from I and to return to it with a circle of pure fifths. — Hucbald.SaintAmand (talk) 20:58, 27 May 2024 (UTC)
- I have no choice but, this time, to agree with you absolutely. My temperament is purely mathematical and hardly any musical. It has always bothered me that the definition of "function" in music has nothing to do with its mathematical meaning. I get over it in various ways. E.g. a) musicians are not mathematicians. b) I assume that degree V is always conceptually accompanied by dominant, so in my mind both degree and function exist at the same time, such as V(dominant). c) For the terms degree and function to be so confused, in my opinion, their spaces must be dual. For this to be the case, musicians must limit themselves to considering that the sequence of any two different degrees produces a unique result, such as the result Cad=V-I. Then the degree V can be seen as a function with V(I)=Cad, and also the degree I can be seen as a function with I(V)=Cad. Even so, however, "functional succession" is not easily justified. If I define the composition IV○V as "functional succession" IV•V(I)=IV-V-I, then the duality of degrees and functions is lost and the usual synonymous use of the terms becomes unjustified.
- Recalling that the term "functional succession" is, perhaps for the above reasons, already in quotation marks, I fully agree with your comment, exactly as you put it.
- Translated with DeepL.com (free version) Jimishol (talk) 05:48, 28 May 2024 (UTC)
Circle or cycle?
[edit]A recent modification by user 71.17.203.128 (what a strange name!), already reverted, raised once again the question of "circle" vs "cycle," already discussed on several occasions in this talk page. There are reasons to prefer "circle" which may be more common in English – the situation would be the opposite, say, in French. But I do believe that adding a word about this in the article could prevent further discussions. "Cycle" is used at least three times in the article, but not all three cases may be justifiable. Something should be done about this. Whaddya think? — Hucbald.SaintAmand (talk) 08:17, 22 June 2024 (UTC)
- Cycle might make more sense, as IP user suggested, but lots of things in music don't make sense, e.g. a third is twice as big as a second. I've never heard any musician say "cycle of fifths." Is there a source which does? —Wahoofive (talk) 15:27, 22 June 2024 (UTC)
- @Wahoofive, I don't mean that we should replace "circle" by "cycle", merely that we should say that "cycle" is a possible variant. This should close the discussion. Sources are not lacking:
- Our article itself uses "cycle" three times:
- "It was known in [A]ntiquity that a cycle of twelve fifths was almost exactly seven octaves" – cycle is preferred here because the idea is to stress the origin of the (Pythagorean) comma, i.e. that the series does not close on itself as a circle.
- "Cycle' appears in a quotation from A. Whitall in The Oxford Companion to Music (see note 17), which I was unable to check.
- It also appears about a quotation from R. Scruton, The Ring of Truth: The Wisdom of Wagner's Ring of the Nibelung (see note 20), but the truth is that Scruton never writes "cycle or fifths" and only once "circle of fifths" (p. 174, about circles of third progressions replacing it in Schubert).
- In my own electronic library, I find "cycle of fifths" many times, among others in
- E. Amiot (2016), Music Through Fourier Space.
- W. Apel (1950), Harvard Dictionary of Music (s.v. "Chinese Music").
- Th. Christensen (2019), Stories of Tonality in the Age of François-Joseph Fétis.
- S. Clark (2011), "On the Imagination of Tone in Schubert's Liedesend [etc.]", in The Oxford Handbook of Neo-Riemannian Music Theories.
- D. Conklin & S. Weisser, "Pattern and Antipattern Discovery in Ethiopian Bagana Song", in Computational Analysis.
- E. Kurth (1991), Selected Writings.
- L. Meyer (1973), Explaining Music.
- N. Newton (2019), "Chromatic Linear Progressions in Popular Music", in The Routledge Companion to Popular Music Analysis.
- C. Sachs (1943), The Rise of Music in the Ancient World.
- N. Waltham-Smith (2019), "Sequence", The Oxford Handbook of Critical Concepts in Music Theory.
Etc.
- Scholar Google gives about 1990 replies for "cycle of fifths", as against about 9130 for "circle of fifths" (i.e. a relation of about 20% for the first). In French, about 414 results for "cycle des quintes", as against 60 only for "cercle des quintes" (80% for the first – the situation is the reverse from that in English).
- Our article itself uses "cycle" three times:
- Hucbald.SaintAmand (talk) 11:40, 23 June 2024 (UTC)
- I should have noted, in addition, that the French article corresponding to this one on FR.WP is "Cycle des quintes"; this may be a typically French usage, other European languages prefer "circle" or its equivalent. — Hucbald.SaintAmand (talk) 16:05, 24 June 2024 (UTC)
- @Wahoofive, I don't mean that we should replace "circle" by "cycle", merely that we should say that "cycle" is a possible variant. This should close the discussion. Sources are not lacking:
- Comment: The normal name is "circle of fifths"; no problem in also using the word "cycle" appropriately as well in the article. But I do not think it is an improvement to start one of those ridiculous WPrambles, listing all sorts of "alternative names" in other languages, scripts, obscure/deprecated/wrong Unicode characters that might have something to do with it etc etc etc... Meanwhile this comment strikes me as bizarre: "cycle is preferred here because the idea is to stress the origin of the (Pythagorean) comma, i.e. that the series does not close on itself as a circle." But the meaning of "cycle" is (at least in its mathematical sense) precisely that of a closed cycle, otherwise it would not be a cycle. The CoF is isomorphic to the cyclic group of order 12, whose multiplication table can be used to convert semitones to CoF positions, for example. So arguably "cycle of fifths" might have been a better term, just as "cheap at twice the price" would have been better than the usual expression. Imaginatorium (talk) 07:03, 2 July 2024 (UTC)
- We are not "starting" a ridiculous ramble (it started long ago), we are trying to close it. Could we agree that while the main term is "circle", "cycle" is a possible variant, and say so somewhere in the article? – Hucbald.SaintAmand (talk) 11:38, 2 July 2024 (UTC)
- I'm fine with this. —Wahoofive (talk) 15:25, 2 July 2024 (UTC)
- I added five words at the beginning of the article, which (I hope) should close the discussion. But feel free to formulate this otherwise. I don't think references are needed, the list of sources above will remain available. — Hucbald.SaintAmand (talk) 21:16, 2 July 2024 (UTC)
- I'm fine with this. —Wahoofive (talk) 15:25, 2 July 2024 (UTC)
- We are not "starting" a ridiculous ramble (it started long ago), we are trying to close it. Could we agree that while the main term is "circle", "cycle" is a possible variant, and say so somewhere in the article? – Hucbald.SaintAmand (talk) 11:38, 2 July 2024 (UTC)

